
The line segment joining the points (3, -4) and (1,2) is trisected at the points P and Q. If the coordinates of P and Q are (p, -2) and ( $\dfrac{5}{3}$, q) respectively, find the values of p and q.
A. p = $\dfrac{7}{3}$
B. p = 0
C. q = 0
D. q = $\dfrac{7}{3}$
Answer
600.6k+ views
Hint: In this question to find the values of p and q, we will use the section formula and then check each given option to find out which are correct. After solving by section formula we equate the coordinates with given points.hence we can get the value of p and q.
Complete step-by-step solution:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let say A (3, -4) and B (1,2) makes a line segment AB. The line segment AB is trisected at points P and Q. So, we will apply section formula both at point P and Q. As, P divides line segment AB in ratio 1:2.
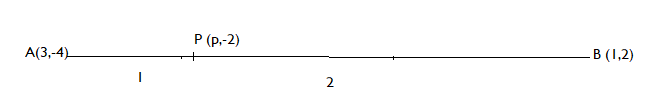
So, applying section formula at point P (p, -2), we get
x – coordinate of P = $\dfrac{{1(1){\text{ + 2(3)}}}}{3}$ = $\dfrac{7}{3}$
$ \Rightarrow $ p = $\dfrac{7}{3}$
As, Q divides the line segment AB in the ratio 2:1.
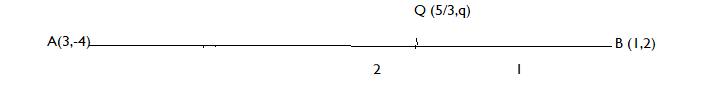
Applying section formula at point Q ( $\dfrac{5}{3}$, q), we get
y – coordinate of Q = $\dfrac{{2(2){\text{ + 1( - 4)}}}}{3}$ = 0
$ \Rightarrow $ q = 0
So, the correct options are (A) and (C).
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Complete step-by-step solution:
Now, we will use the section formula. The section formula tells us the coordinates of a point which divides a given line segment into two parts such that their lengths are in the ratio m: n. The Section formula to find a point (x, y) is
x = $\dfrac{{{\text{m}}{{\text{x}}_2}{\text{ + n}}{{\text{x}}_1}}}{{{\text{m + n}}}}$
y = $\dfrac{{{\text{m}}{{\text{y}}_2}{\text{ + n}}{{\text{y}}_1}}}{{{\text{m + n}}}}$
Here we are given two points. Let say A (3, -4) and B (1,2) makes a line segment AB. The line segment AB is trisected at points P and Q. So, we will apply section formula both at point P and Q. As, P divides line segment AB in ratio 1:2.
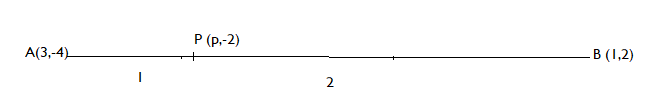
So, applying section formula at point P (p, -2), we get
x – coordinate of P = $\dfrac{{1(1){\text{ + 2(3)}}}}{3}$ = $\dfrac{7}{3}$
$ \Rightarrow $ p = $\dfrac{7}{3}$
As, Q divides the line segment AB in the ratio 2:1.
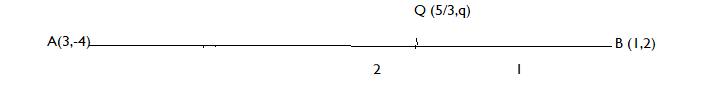
Applying section formula at point Q ( $\dfrac{5}{3}$, q), we get
y – coordinate of Q = $\dfrac{{2(2){\text{ + 1( - 4)}}}}{3}$ = 0
$ \Rightarrow $ q = 0
So, the correct options are (A) and (C).
Note: While solving such types of questions, it is important to apply the section formula correctly. Most of the students made a mistake while applying the section formula. They replaced m from n and n from m. Also, apply the proper ratio for finding the coordinates of a point. Also, when only you have to find the value of a given variable, apply only that formula to find the value of the variable, for example if you are given that the x – coordinate of point is k, so you have to apply only the formula to find the x – coordinate of point.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




