Question

The lengths of the sides of a triangle are 6,10 and 14. How do you find the perimeter of the triangle formed by joining the midpoints of these sides?

Answer 1

Hint: First we will draw a diagram of the triangle with side lengths 6, 10 and 14. Then by using the midpoint property we will draw another triangle and then by using the formula of perimeter we will calculate the perimeter of the triangle.

Complete step by step solution:
The perimeter of a triangle is given as the sum of all three sides of the triangle.
We have been given that the lengths of the sides of a triangle are 6,10 and 14. A triangle is formed by joining the midpoints of these sides.
We have to find the perimeter of the triangle formed by joining the midpoints of sides 6, 10 and 14.
Now, let us first draw a diagram, then we will get

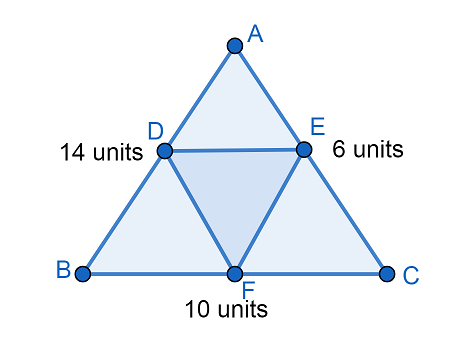
Let the length of side AC is 6 units, length of side BC is 10 units and length of side AB is 14 units. The midpoints of sides AB, BC and AC are D, F and E respectively. By joining the midpoints we draw a triangle DEF.
Now, we know that midpoints bisect the side into two equal halves. So we will get
$\Rightarrow AD=BD=7units,AE=EC=3units,BF=FC=5units$
Now, we know that by midpoint theorem “the line segment in a triangle joining the midpoint of two sides of a triangle is parallel to its third side and half of the length of the third side.
So we get $DE=5units,EF=7units,DF=3units$
Now, we know that the perimeter of the triangle is equal to the sum of all sides of a triangle.
So the perimeter of $\Delta DEF=DE+DF+EF$
Now, substituting the values we will get
$\begin{align}
  & \Rightarrow \text{Perimeter of }\Delta DEF=5+7+3 \\
 & \Rightarrow \text{Perimeter of }\Delta DEF=15units \\
\end{align}$
Hence we get the perimeter of the triangle as 15 units.

Note: Alternatively we can use the similarity property of triangles. We prove both the triangles similar and then by using the properties of similar triangles we will find the lengths of the sides of the triangle and then by substituting the values in the formula we will find the perimeter.