Question

The length of the latus rectum of the parabola ${\text{169 [(x - 1}}{{\text{)}}^2}{\text{ + (y - 3}}{{\text{)}}^2}]{\text{ = (5x - 12y + 17}}{{\text{)}}^2}$ is
A. $\dfrac{{14}}{{13}}$
B. $\dfrac{{12}}{{13}}$
C. $\dfrac{{28}}{{13}}$
D. None of these

Answer 1

Hint: To solve this question we will use the definition of parabola and we will go through the basics to find the value of the latus rectum of the given parabola.

Complete step-by-step answer:

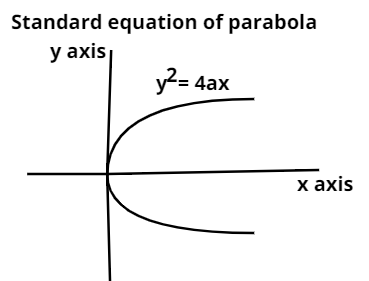
Now, a conic section is called parabola if the distance of a point P (x, y) from the focus of parabola is equal to the distance of point P from the directrix of parabola. If the parabola is ${{\text{y}}^2}{\text{ = 4ax}}$, having focus at (a, 0) and its directrix is x + a = 0 , so according to the definition of parabola for a point P lying on parabola, we get

$\sqrt {{{{\text{(x - a)}}}^2}{\text{ + (y - 0}}} {)^2}{\text{ = }}\left| {\dfrac{{{\text{x +
a}}}}{1}} \right|$ ……. (1)

Now, given equation is ${\text{169 [(x - 1}}{{\text{)}}^2}{\text{ + (y -
3}}{{\text{)}}^2}]{\text{ = (5x - 12y + 17}}{{\text{)}}^2}$. It can be written as

${\text{[(x - 1}}{{\text{)}}^2}{\text{ + (y - 3}}{{\text{)}}^2}]{\text{ = }}\dfrac{{{{{\text{(5x -
12y + 17)}}}^2}}}{{169}}$
Taking under – root both sides, we get
$\sqrt {{{{\text{(x - 1)}}}^2}{\text{ + (y - 3}}{{\text{)}}^2}} {\text{ = }}\left|

{\dfrac{{{\text{5x - 12y + 17}}}}{{\sqrt {{{(5)}^2}{\text{ + ( - 12}}{{\text{)}}^2}} }}} \right|$

So, comparing the above equation with the equation (1), we get

Focus is F (1, 3) and the equation of the directrix is 5x – 12y + 17 = 0.

Now, Length of latus rectum = 4a

Also, latus rectum = 2 (distance between the focus and the directrix)

So, latus rectum = $2\left| {\dfrac{{5(1){\text{ - 12(3) + 17}}}}{{\sqrt {{5^2}{\text{ + ( -
12}}{{\text{)}}^2}} }}} \right|$

Latus rectum = $2{\text{ }} \times {\text{ }}\dfrac{{14}}{{13}}{\text{ = }}\dfrac{{28}}{{13}}$

So, option (C) is the correct answer.

Note: When we come up with such types of questions, we will go through the basics of conic section. It is the easiest way to solve such problems. We have to use the definition of conic sections and compare the given equation with the standard equation to get the value of focus, vertex of parabola. You should take care of the formulas. Many students make mistakes while finding the length of focus from the directrix. They apply the wrong formula which results in incorrect answers.