Question

The length of the diagonal of the square is $\sqrt 2 \left( {6 + 2\sqrt 5 } \right)$ cm. Then find the length of a side of the square.

Answer 1

Hint: In this question, we use the formula of Pythagoras theorem. We know in square all four interior angles are equal to 900. So, we can easily use Pythagoras theorem in which diagonal as a hypotenuse and perpendicular and base are sides of square.

Complete step-by-step answer:

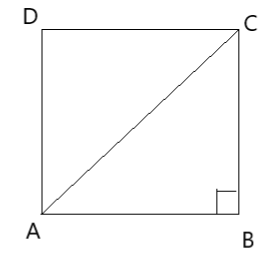
Consider a square ABCD of side x in which diagonal AC and right angle at B.
Given, length of diagonal of square $AC = \sqrt 2 \left( {6 + 2\sqrt 5 } \right)$
Now, use of Pythagoras theorem in $\vartriangle ABC$ and right angle at B.
${\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}$
We know in square all sides are equal, $AB = BC = CD = DA = x$
$
   \Rightarrow {\left( {AC} \right)^2} = {\left( x \right)^2} + {\left( x \right)^2} \\
   \Rightarrow {\left( {AC} \right)^2} = 2{x^2} \\
   \Rightarrow {x^2} = \dfrac{{{{\left( {AC} \right)}^2}}}{2} \\
$
Taking square root on both sides
$ \Rightarrow x = \dfrac{{AC}}{{\sqrt 2 }}$
We know value of $AC = \sqrt 2 \left( {6 + 2\sqrt 5 } \right)$
$
   \Rightarrow x = \dfrac{{\sqrt 2 \left( {6 + 2\sqrt 5 } \right)}}{{\sqrt 2 }} \\
   \Rightarrow x = \left( {6 + 2\sqrt 5 } \right)cm \\
$
So, the length of a side of the square is $\left( {6 + 2\sqrt 5 } \right)$ cm.

Note: Whenever we face such types of problems we use some important points. Like we use the Pythagoras theorem to make a relation between diagonal and sides of a square then put the value of diagonal in relation. So, after calculation we will get the required answer.