Question

The length of the chord of a circle is 8 cm and the perpendicular distance between centre of the circle and the chord is 3 cm. Then the radius of the circle is equal to?
(a) 4 cm
(b) 5cm
(c) 6cm
(d) 8cm

Answer 1

Hint: First, we will draw the circle and mark the centre as A and chord as BC. Then, we will use the concept of Pythagoras theorem and apply it on the formed triangle $\Delta ABD$. While using the theorem we will take the half of the chord so that we will substitute the required value in the Pythagoras equation.

Complete step-by-step answer:
The diagram of the question is given below.

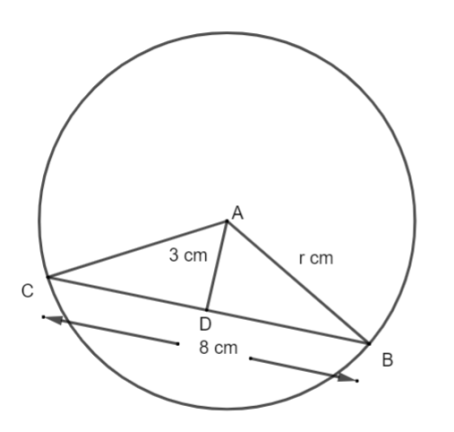
According to the figure we have a chord namely, BC = 8 cm and the distance from the centre and the chord represented by AD is 3 cm. This further results into the new length of DB is the half of CB. Thus we have DB = 4 cm. We are supposed to find the value of AB which is the radius of the circle. For this we will consider the triangle $\Delta ABD$ and we are going to apply the Pythagoras theorem here. This is because we have $\angle ADB={{90}^{\text{o}}}$. This result into
\[\begin{align}
  & A{{B}^{2}}=A{{D}^{2}}+D{{B}^{2}} \\
 & \Rightarrow {{r}^{2}}={{\left( 3cm \right)}^{2}}+{{\left( 4cm \right)}^{2}} \\
 & \Rightarrow {{r}^{2}}=9c{{m}^{2}}+16c{{m}^{2}} \\
 & \Rightarrow {{r}^{2}}=25c{{m}^{2}} \\
 & \Rightarrow r=\pm 5cm \\
\end{align}\]
So, clearly we get the two values of r which are given as + 5cm or – 5cm. As we know that the radius cannot be negative therefore, we will reject r as – 5cm and thus we will have that r = 5cm.
Hence, the correct option is (b).
Note: We can also solve it by using another alternate method. We will take AC as the radius of the circle. After this in this method, we will apply the Pythagoras theorem on the triangle $\Delta ACD$ and we are going to apply the Pythagoras theorem here. This is because we have $\angle ADC={{90}^{\text{o}}}$. This results into r = 5cm only. We will focus while performing calculations. If we solve it without focus the answer will get wrong. We have applied the Pythagoras theorem here because of the presence of ${{90}^{\text{o}}}$ angle.