Question

The length, breadth and height of a room are 5m, 4m and 3m respectively. Find the cost of white washing the walls of the room and the ceiling at the rate of Rs 7.50 per sq m.

Answer 1

Hint: To solve the question given above, we will first find out the total area which is to be white washed. We will calculate this area by first calculating the area of the ceiling which is rectangular in shape. Then we will calculate the area of four walls which are also rectangular in shape. Then we will add all the areas to get the total area. Then we will multiply this by 7.50 to get the total cost of white washing.

Complete step-by-step answer:
Before solving the question, we are going to assume that the room is cuboidal in shape and the walls, roof and base are rectangular in shape. The rough sketch of the room is shown below:

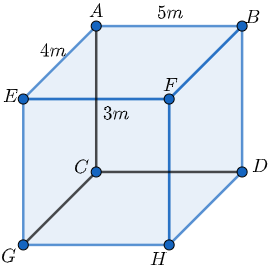
Here, we can see that ABEF is the roof (ceiling), GCDH is the base and ABDC, ACGE, EGHF and BDHF are the walls of the room. AC is the height of the room, AB is the length of the room and AE is the breadth of room.
Now, first we have to calculate the total area in which we want to do white washing. The total area will be equal to the area of ceiling and area of four walls. So we will calculate each area one by one. The area of each of them will be equal to the area of the rectangle because each face of the cuboid is rectangular in shape. The area of rectangle with adjacent sides a and b is given by:
$Area=a\times b$
The area of ceiling $ABEF=AB\times AE$
$Area\text{ }of\text{ }ABEF=5m\times 4m$
\[Area\text{ }of\ ABEF=20{{m}^{2}}.........\left( 1 \right)\]
\[\begin{align}
  & Area\text{ }of\text{ }wall~ABDC=AB\times AC \\
 & Area\text{ }of\text{ }wall~ABDC=5m\times 3m \\
 & Area\text{ }of\text{ }wall~ABDC=15{{m}^{2}}........\left( 2 \right) \\
\end{align}\]
\[\begin{align}
  & Area\text{ }of\text{ }wall~ACGE=AC\times AE \\
 & Area\text{ }of\text{ }wall~ACGE=3m\times 4m \\
 & Area\text{ }of\text{ }wall~ACGE=12{{m}^{2}}........\left( 3 \right) \\
\end{align}\]
\[\begin{align}
  & Area\text{ }of\text{ }wall~EGFH=EG\times EF \\
 & Area\text{ }of\text{ }wall~EGFH=3m\times 5m \\
 & Area\text{ }of\text{ }wall~EGFH=15{{m}^{2}}.........\left( 4 \right) \\
\end{align}\]
\[\begin{align}
  & Area\text{ }of\text{ }wall~BDHF=BD\times FB \\
 & Area\text{ }of\text{ }wall~BDHF=3m\times 4m \\
 & Area\text{ }of\text{ }wall~BDHF=12{{m}^{2}}........\left( 5 \right) \\
\end{align}\]
Thus, the total area will be given by:
$\begin{align}
  & Total\ area=\left( Area\text{ }ofABEF \right)+\left( Area\text{ }ofABDC \right)+\left( Area\text{ }ofACGE \right)+ \\
 & \text{ }\left( Area\text{ }ofEGFH \right)+\left( Area\text{ }ofBDHF \right) \\
 & Total\ area=20{{m}^{2}}+15{{m}^{2}}+12{{m}^{2}}+15{{m}^{2}}+12{{m}^{2}} \\
 & Total\ area=74{{m}^{2}} \\
\end{align}$
Now, the cost of white washing $1{{m}^{2}}area=Rs7.50$
So the cost of white washing $74{{m}^{2}}=Rs7.5\times 74$
Thus, total cost of white washing $=Rs555$

Note: The area of the room which needs to be white washed can also be calculated by first calculating the total surface area of the cuboid and then subtracting the area of base from it. Thus, we have:
Required area = Total surface area – area of base
The total surface area of cuboid is given by:
$TSA=2\left( lb+bh+hl \right)$
Thus, we have:

$\begin{align}
  & \Rightarrow Required\text{ }area=2\left( lb+bh+hl \right)-area\text{ }of\ GCHD \\
 & \Rightarrow Required\text{ }area=2\left[ \left( 5 \right)\left( 4 \right)+\left( 4 \right)\left( 3 \right)+\left( 3 \right)\left( 5 \right) \right]-\left( 5 \right)\left( 4 \right) \\
 & \Rightarrow Required\text{ }area=2\left[ 20+12+15 \right]-20 \\
 & \Rightarrow Required\text{ }area=2\left[ 47 \right]-20 \\
 & \Rightarrow Required\text{ }area=94-20 \\
 & \Rightarrow Required\text{ }area=74{{m}^{2}} \\
\end{align}$