Question

The largest possible sphere is carved out of a wooden solid cube of side 7 cm. Find the volume of the wood left.$$[use\ \pi =\dfrac{22}{7} ]$$

Answer 1

Hint: In this question it is given that the largest possible sphere is carved out of a wooden solid cube of side 7 cm. We have to find the volume of the wood left. So to find the solution we have to identify what should be the diameter for which the getting sphere will be the largest and once we got the diameter then we can easily find the volume of wood left, i.e, volume wood left = Volume of cube - volume of sphere.

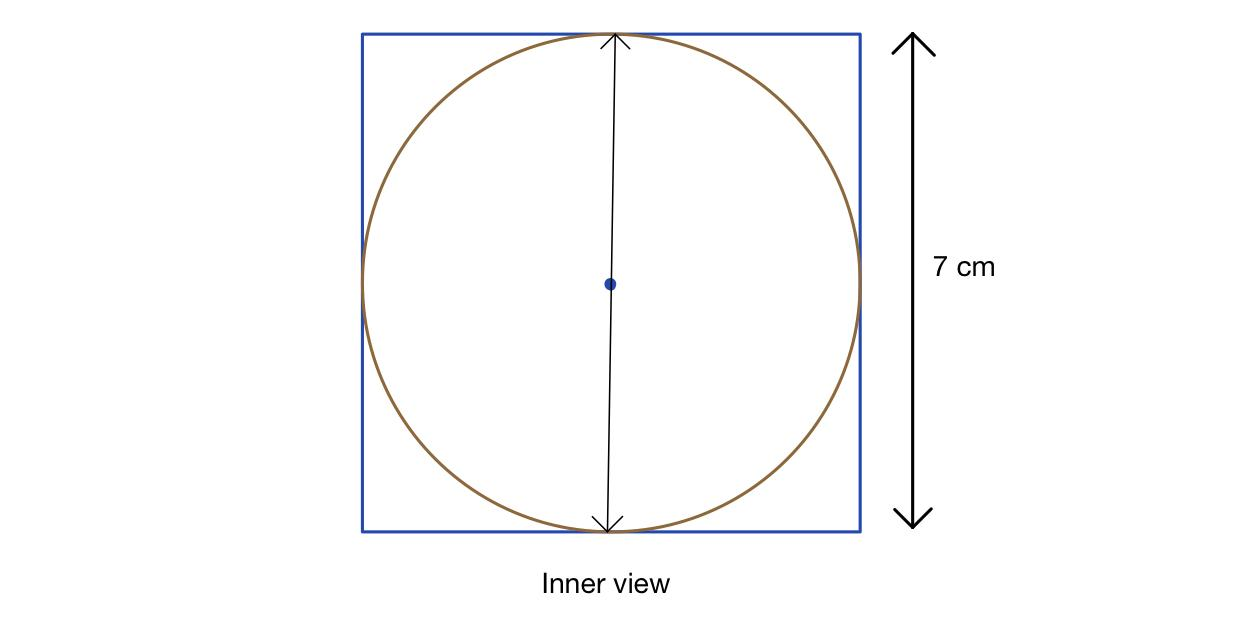
So for this we can say that the diameter of the largest sphere is equal to the side of the cube.
Complete step-by-step solution:
So since the side of the given cube is 7cm then the diameter of the largest possible sphere must be the side of the cube.,
i.e, diameter of the sphere = side of cube =7cm
Then the radius of the sphere(r)=$$\dfrac{diameter}{2} =\dfrac{7}{2} cm$$.
Now as we know that the volume of a sphere,
$$V_{1}=\dfrac{4}{3} \pi r^{3}$$
     =$$\dfrac{4}{3} \times \dfrac{22}{7} \times \left( \dfrac{7}{2} \right)^{3} $$
     =$$\dfrac{539}{3}cm^{3}$$
And the volume of cube
$V_{2}$=$\left( side\right)^{3} $=$7^{3}$=343$cm^{3}$
Therefore, Volume of wood left = Volume of cube - volume of sphere
V=$$V_{2}-V_{1}$$=(343-$$\dfrac{539}{3}$$) $cm^{3}$ =(343-179.67) $cm^{3}$=163.33 $cm^{3}$.
Which is our required solution.
Note: It is not possible to draw a three dimensional shape so that is why we have only drawn the inner portion, i.e, if you cut the cube in half then this will give the picture.