Question

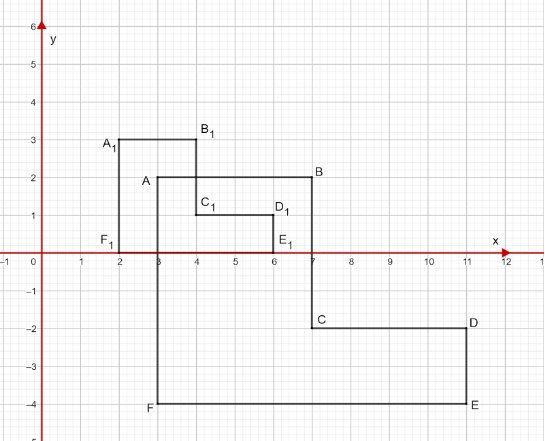
The L – shaped \[{A_1}{B_1}{C_1}{D_1}{E_1}{F_1}\] is the image of L – shaped ABCDEF after which of the following resizing?

A. Scale factor \[\dfrac{1}{2}\] with central point \[(1,4)\]
B. Scale factor \[2\] with central point \[(0,5)\]
C. Scale factor with central point \[(2,3)\]
D. Scale factor \[2\] with central point \[(1,4)\]

Answer 1

Hint: Here in this question they have not asked directly what we have to determine. By looking at the options we came to know that we have to determine the scale factor and central point. First by considering the ratio of the length of the resized image to the actual image. We can determine the scale factor. Then by extending the lines from the point \[A{A_1}\] and from \[B{B_1}\], the point of intersection will be the central point.

Complete step by step answer:
In general, the resizing means resizing is altering the size of your image without cutting anything out. To resize an image is to essentially change the file size. Because sometimes, size does matter. Resizing can help your photo fit into a certain space on a screen, such as in a blog post or social media post.

Now consider the given question, here we can see the two L – shaped figures. The \[{A_1}{B_1}{C_1}{D_1}{E_1}{F_1}\] is a resized image of the L – shaped \[ABCDEF\]. Here we have to determine the scale factor and the central point. To find the scale factor we have to find the ratio of the resized image to the actual image. Here each box is considered as the one unit. We determine the scale factor for each line segment. Now we determine the scale factor for the line $AB$.
\[ \Rightarrow \dfrac{{{A_1}{B_1}}}{{AB}} = \dfrac{2}{4}\]
On simplifying we have
\[ \Rightarrow \dfrac{{{A_1}{B_1}}}{{AB}} = \dfrac{1}{2}\]
Now we determine the scale factor for the line BC.
\[ \Rightarrow \dfrac{{{B_1}{C_1}}}{{BC}} = \dfrac{2}{4}\]
On simplifying we have
\[ \Rightarrow \dfrac{{{B_1}{C_1}}}{{BC}} = \dfrac{1}{2}\]

Now we determine the scale factor for the line CD.
\[ \Rightarrow \dfrac{{{C_1}{D_1}}}{{CD}} = \dfrac{2}{4}\]
On simplifying we have
\[ \Rightarrow \dfrac{{{C_1}{D_1}}}{{CD}} = \dfrac{1}{2}\]
Now we determine the scale factor for the line DE.
\[ \Rightarrow \dfrac{{{D_1}{E_1}}}{{DE}} = \dfrac{1}{2}\]
Now we determine the scale factor for the line EF.
\[ \Rightarrow \dfrac{{{E_1}{F_1}}}{{EF}} = \dfrac{4}{8}\]
On simplifying we have
\[ \Rightarrow \dfrac{{{E_1}{F_1}}}{{EF}} = \dfrac{1}{2}\]
Now we determine the scale factor for the line AF.
\[ \Rightarrow \dfrac{{{A_1}{F_1}}}{{AF}} = \dfrac{3}{6}\]
On simplifying we have
\[ \Rightarrow \dfrac{{{A_1}{F_1}}}{{AF}} = \dfrac{1}{2}\]
Therefore the scale factor is \[\dfrac{1}{2}\]. Now we have to determine the central point. To find this we have to extend the line from \[A{A_1}\] and from \[B{B_1}\], and we check at which point these two lines meet.

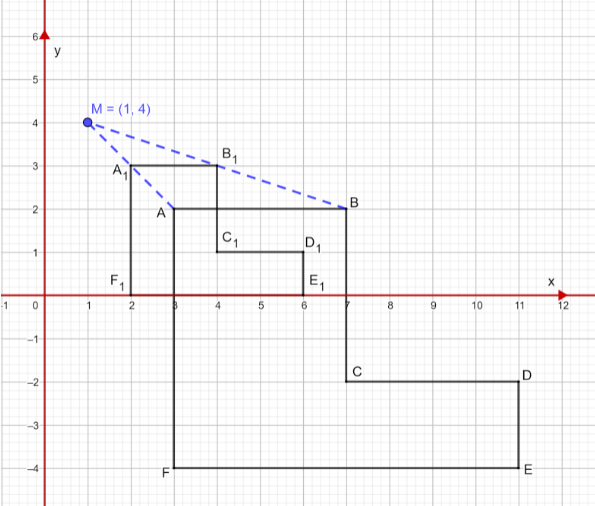
The lines meet at the point \[(1,4)\]. Therefore the central point is \[(1,4)\]. Hence the scale factor \[\dfrac{1}{2}\] with a central point \[(1,4)\].

Hence, the option A is the correct one.

Note:A scale factor in math is the ratio between corresponding measurements of an object and a representation of that object. If the scale factor is a whole number, the copy will be larger. If the scale factor is a fraction, the copy will be smaller. Here in this question the resize image is smaller when we compare it to the actual image.