Question

The intersection of a sphere by a plane is:
(a) Line
(b) Circle
(c) Plane
(d) Sphere

Answer 1

Hint: As we are given the intersection of the circle and the plane so first thing we will do is take the equations ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}+{{\left( z-{{z}_{1}} \right)}^{2}}={{R}^{2}}$ and $Ax+By+Cz+D=0$. After solving these together. Here, ${{x}_{1}},{{y}_{1}}$ and ${{z}_{1}}$ are the points of the centre of the sphere and R is the radius of the same sphere. After doing this we will use W = {(x, y, z): x = ${{x}_{1}}$ + At, y = ${{y}_{1}}$ + Bt, z = ${{z}_{1}}$ + Ct} where t is working as a parameter here and use the value of t in this and substitute in the newly formed equation to solve the question further. At one time after applying these we will use the distance formula $d=\sqrt{{{\left( {{x}_{1}}-x \right)}^{2}}+{{\left( {{y}_{1}}-y \right)}^{2}}+{{\left( {{z}_{1}}-z \right)}^{2}}}$ where d is the distance between the tangent and the centre of the circle.

Complete step-by-step answer:
We will consider any sphere of equation ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}+{{\left( z-{{z}_{1}} \right)}^{2}}={{R}^{2}}$ where ${{x}_{1}},{{y}_{1}}$ and ${{z}_{1}}$ are the points of the centre of the sphere and R is the radius of the same sphere. According to the question we have that there comes a plane which intersects the sphere like in the figure shown below.

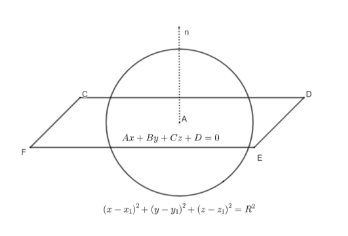
The equation of the plane is $Ax+By+Cz+D=0$ and it forms a normal represented by n as $n=a\hat{i}+b\hat{j}+c\hat{k}$ in the figure.
We need to find out what is formed with the intersection of the plane and the sphere. For that we will take the equation that is formed after this intersection. This can be done with the help of the parametric equations. We can clearly see that the line which passes through the centre of the sphere being as a normal to it will result into the equation W = {(x, y, z): x = ${{x}_{1}}$ + At, y = ${{y}_{1}}$ + Bt, z = ${{z}_{1}}$ + Ct} where t is working as a parameter here and ${{x}_{1}},{{y}_{1}}$ and ${{z}_{1}}$ are the points of the centre of the sphere. Since this equation of the line lies on the plane only therefore we will substitute these points in the equation of the plane. Therefore we get that $Ax+By+Cz+D=0$ becomes $A\left( {{x}_{1}}+At \right)+B\left( {{y}_{1}}+Bt \right)+C\left( {{z}_{1}}+Ct \right)+D=0$. Now we are going to simplify this equation. Therefore, we will get
$\begin{align}
  & A\left( {{x}_{1}}+At \right)+B\left( {{y}_{1}}+Bt \right)+C\left( {{z}_{1}}+Ct \right)+D=0 \\
 & \Rightarrow A{{x}_{1}}+{{A}^{2}}t+B{{y}_{1}}+{{B}^{2}}t+C{{z}_{1}}+{{C}^{2}}t+D=0 \\
\end{align}$
Now we will take t terms on one side and the constants on the other side of the equal sign. Thus, we get
$\begin{align}
  & {{A}^{2}}t+{{B}^{2}}t+{{C}^{2}}t+A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D=0 \\
 & \Rightarrow \left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)t=-\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right) \\
 & \Rightarrow t=\dfrac{-\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)}......(i) \\
\end{align}$
After this we will substitute the value of t as taken out by the equation W = {(x, y, z): x = ${{x}_{1}}$ + At, y = ${{y}_{1}}$ + Bt, z = ${{z}_{1}}$ + Ct} where t is working as a parameter here and ${{x}_{1}},{{y}_{1}}$ and ${{z}_{1}}$ are the points of the centre of the sphere. So, x = ${{x}_{1}}$ + At will become as $t=\dfrac{x-{{x}_{1}}}{A}$ and similarly we will also get $t=\dfrac{y-{{y}_{1}}}{B},t=\dfrac{z-{{z}_{1}}}{C}$. By substituting these values in equation (i) we will get $\begin{align}
  & \dfrac{x-{{x}_{1}}}{A}=\dfrac{-\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},\dfrac{y-{{y}_{1}}}{B}=\dfrac{-\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},\dfrac{z-{{z}_{1}}}{C}=\dfrac{-\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \\
 & \Rightarrow x-{{x}_{1}}=-\dfrac{A\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},y-{{y}_{1}}=-\dfrac{B\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},z-{{z}_{1}}=-\dfrac{C\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \\
 & \Rightarrow x={{x}_{1}}-\dfrac{A\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},y={{y}_{1}}-\dfrac{B\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)},z={{z}_{1}}-\dfrac{C\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \\
\end{align}$
Now we will apply the formula of the distance between the centre of the circle and the tangent where we are considering the tangent as one of the lines of the plane. The formula is given by
$\begin{align}
  & d=\sqrt{{{\left( {{x}_{1}}-x \right)}^{2}}+{{\left( {{y}_{1}}-y \right)}^{2}}+{{\left( {{z}_{1}}-z \right)}^{2}}} \\
 & \Rightarrow d=\sqrt{{{\left( {{x}_{1}}-\left( {{x}_{1}}-\dfrac{A\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right) \right)}^{2}}+{{\left( {{y}_{1}}-\left( {{y}_{1}}-\dfrac{B\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right) \right)}^{2}}+{{\left( {{z}_{1}}-\left( {{z}_{1}}-\dfrac{C\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right) \right)}^{2}}} \\
 & \Rightarrow d=\sqrt{{{\left( {{x}_{1}}-{{x}_{1}}+\dfrac{A\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}+{{\left( {{y}_{1}}-{{y}_{1}}+\dfrac{B\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}+{{\left( {{z}_{1}}-{{z}_{1}}+\dfrac{C\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}} \\
 & \Rightarrow d=\sqrt{{{\left( \dfrac{A\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}+{{\left( \dfrac{B\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}+{{\left( \dfrac{C\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}} \\
 & \Rightarrow d=\sqrt{{{\left( \dfrac{\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \right)}^{2}}\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)} \\
 & \Rightarrow d=\sqrt{\dfrac{{{\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}^{2}}}{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)}} \\
 & \Rightarrow d=\dfrac{\left( A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right)}{\sqrt{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)}} \\
\end{align}$
 As the distance cannot be negative therefore we will write the above equation as $d=\dfrac{\left| \left. A{{x}_{1}}+B{{y}_{1}}+C{{z}_{1}}+D \right| \right.}{\sqrt{\left( {{A}^{2}}+{{B}^{2}}+{{C}^{2}} \right)}}$. As the value of R is greater than d therefore the intersection formed is going to be a circle. This is because after considering the simpler form of the equation of the distance between the centre of the circle and the tangent of the point we are getting a positive Cartesian equation of it.
Hence, the correct option is (b).

Note: As this question contains so many calculations, one should take care that these calculations might get wrong if not solved under complete focus. The figure should be drawn correctly so that we can solve the questions using right equations after understanding the figure. Using the trick of the parametric equation we will be able to solve the question further. After drawing the figure one can get confused between the formation of the figure as a circle or a sphere. But since it is intersected by a plane therefore the figure that is going to come out as common will be a 2 dimensional circle only and not a sphere.