Question

The internal center of similitude of two circles \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\] is
\[\begin{align}
  & \text{(A) (-1,-2)} \\
 & \text{(B) (-2,-1)} \\
 & \text{(C) (3,2)} \\
 & \text{(D) (-5,-6)} \\
\end{align}\]

Answer 1

Hint: We know that if \[P({{x}_{1}},{{y}_{1}})\] and \[Q({{x}_{2}},{{y}_{2}})\] are divided by \[R({{x}_{3}},{{y}_{3}})\] in the ratio \[m:n\] internally if \[{{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},{{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\]. We should know that if the internal centre of similitude of two circles \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2},{{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}\] is \[A({{x}_{3}},{{y}_{3}})\], then \[A({{x}_{3}},{{y}_{3}})\] divides the centre of two circles in the ratio \[{{r}_{1}}:{{r}_{2}}\]. By using this concept, we can find the internal centre of similitude of \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\].

Complete step by step solution:
We know that if the internal centre of similitude of two circles \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2},{{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}\] is \[A({{x}_{3}},{{y}_{3}})\], then \[A({{x}_{3}},{{y}_{3}})\] divides the centre of two circles in the ratio \[{{r}_{1}}:{{r}_{2}}\] .

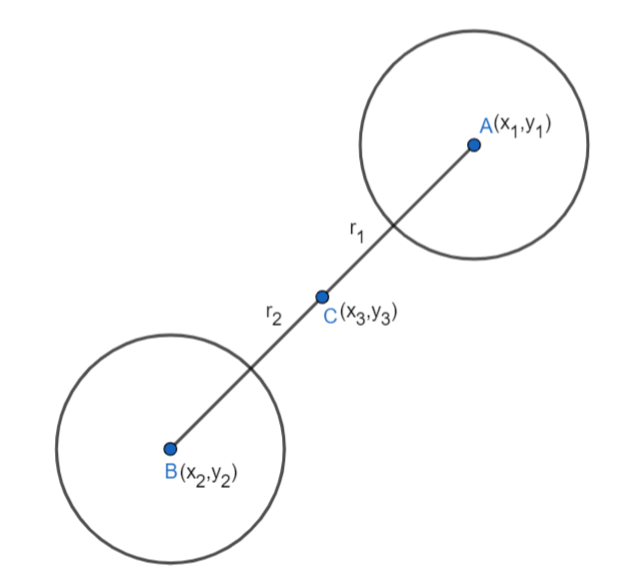
In the question, we were given two circles \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9,{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\].
Now let us compare \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9\] with \[{{(x-{{x}_{1}})}^{2}}+{{(y-{{y}_{1}})}^{2}}=r_{1}^{2}\].
We get
\[\begin{align}
  & {{x}_{1}}=3....(1) \\
 & {{y}_{1}}=2.....(2) \\
 & {{r}_{1}}^{2}=9 \\
 & \Rightarrow {{r}_{1}}=3....(3) \\
\end{align}\]
Now let us compare \[{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\] with \[{{(x-{{x}_{2}})}^{2}}+{{(y-{{y}_{2}})}^{2}}=r_{2}^{2}\].
We get
\[\begin{align}
  & {{x}_{2}}=-5...(4) \\
 & {{y}_{2}}=-6.....(5) \\
 & {{r}_{2}}^{2}=9 \\
 & \Rightarrow {{r}_{2}}=3....(6) \\
\end{align}\]
We know that the internal centre of similitude divides the line joining the centre in the ratio \[{{r}_{1}}:{{r}_{2}}\] internally.
So, we get the centre of \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9\] is \[{{C}_{1}}(3,2)\] and radius of \[{{(x-3)}^{2}}+{{(y-2)}^{2}}=9\] is equal to 3.
In the similar manner, we get centre of \[{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\] is \[{{C}_{2}}(-5,-6)\] and radius of \[{{(x+5)}^{2}}+{{(y+6)}^{2}}=9\] is equal to 3.
So, it is clear that \[A({{x}_{3}},{{y}_{3}})\] divides \[{{C}_{1}}(3,2)\] and \[{{C}_{2}}(-5,-6)\] in the ratio \[3:3\] internally.
We know that if \[P({{x}_{1}},{{y}_{1}})\] and \[Q({{x}_{2}},{{y}_{2}})\] are divided by \[R({{x}_{3}},{{y}_{3}})\] in the ratio \[m:n\] internally if \[{{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n},{{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n}\].
By using this concept, we get
\[\begin{align}
  & \Rightarrow {{x}_{3}}=\dfrac{m{{x}_{2}}+n{{x}_{1}}}{m+n} \\
 & \Rightarrow {{x}_{3}}=\dfrac{3(-5)+3(3)}{3+3} \\
 & \Rightarrow {{x}_{3}}=-1.....(7) \\
\end{align}\]
In the similar way, we get
\[\begin{align}
  & \Rightarrow {{y}_{3}}=\dfrac{m{{y}_{2}}+n{{y}_{1}}}{m+n} \\
 & \Rightarrow {{y}_{3}}=\dfrac{3(-6)+3(2)}{3+3} \\
 & \Rightarrow {{y}_{3}}=-2.....(8) \\
\end{align}\]
From equation (7) and equation (8), we get the coordinates of internal centre of similitude is \[(-1,-2)\].
Hence, option A is correct.

Note: Some students have a misconception that if \[P({{x}_{1}},{{y}_{1}})\] and \[Q({{x}_{2}},{{y}_{2}})\] are divided by \[R({{x}_{3}},{{y}_{3}})\] in the ratio \[m:n\] internally if \[{{x}_{3}}=\dfrac{m{{x}_{2}}-n{{x}_{1}}}{m-n},{{y}_{3}}=\dfrac{m{{y}_{2}}-n{{y}_{1}}}{m-n}\]. But we know that the given coordinates are the coordinates obtained if \[R({{x}_{3}},{{y}_{3}})\] is get divided in the ratio \[m:n\] externally. But if this misconception is followed, then we will get the external centre of similitude. But we want internal central similitude. So, this misconception hasto be avoided.