Question

The internal bisector of an angle of a triangle divides the opposite side internally in the ratio of corresponding sides containing angles. Prove it.

Answer 1

Hint: To solve this problem we need to have a basic knowledge about the properties of triangles and Thales theorem and a basic idea about the construction part which helps us to solve the problem in a simple way by using the required theorems.

Complete step-by-step answer:

Let us consider a triangle ABC.
Here AD is the internal bisector of $\angle BAC$ which meets BC at D.
According to the question given
We have to prove that $\dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}$
Now here let us do a simple construction which helps to prove the above condition.
Construction: Draw $CE\parallel DA$ to meet BA which produces at E.

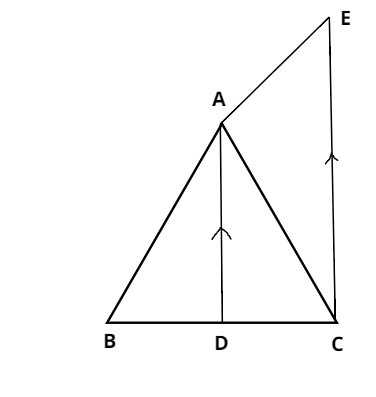
After the construction part is done, we can say that
     $CE\parallel DA$ and AC is the transversal (By construction)
     $\angle DAC = \angle ACE - - - - (1)$ (Alternate angles)
    $\angle BAD = \angle AEC - - - - - (2)$ (Corresponding angles)
Since AD is the angle bisector of $\angle A$
Therefore we can say that $\angle BAD = \angle DAC - - - - - > (3)$
So from (1) (2) and (3) we say that
$\angle ACE = \angle AEC$
Now from triangle $\Delta ACE$
$ \Rightarrow AE = AC$ (Therefore sides opposite to equal angles are equal)
Again now from triangle BCE
$ \Rightarrow CE\parallel DA$
$ \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{{BA}}{{AE}}$ (By using Thales theorem)
$ \Rightarrow \dfrac{{BD}}{{DC}} = \dfrac{{AB}}{{AC}}$ (Since we know that AE=AC)
Hence we have proved that the internal bisector of an angle of a triangle divides the opposite side internally in the ratio of corresponding sides containing angles.

NOTE: This question is generally a theorem type question that we have to prove by considering the required concepts. For this type of proof question we have to do required construction to prove the condition. We generally take other theorems to prove the given theorem, in this theorem we have used Thales theorem and some required properties of triangles.