Question

The intercept made by the circle ${{x}^{2}}+{{y}^{2}}-5x-14=0$ . Find the radius circle. Does this circle exist in real? Justify your answer.

Answer 1

Hint:Compare the given equation with the standard equation of circle i.e. ${{x}^{2}}+{{y}^{2}}+2gxf+2fy+c=0$ where centre (-g, -f) and radius is calculated as $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ . And intercepts on x-axis and y-axis are given as $2\sqrt{{{g}^{2}}-c},2\sqrt{{{f}^{2}}-c}$ respectively. General equation of conic i.e.
$a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0$
Will represent a circle if,
$\Delta \ne 0,a=b,h=0$
Value of $\Delta $ is given as:
$\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}$ .

Complete step-by-step answer:
Given equation of the circle in the problem is
${{x}^{2}}+{{y}^{2}}-5x-14=0............\left( i \right)$
As we know standard equation of a circle can be given by equation as
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0............\left( ii \right)$
Where (-g, -f) is the centre of the circle and $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ will give radius of the circle. And we also know the formula for the intercept made by the circle with equation given in equation (ii) as
‘x’ intercept by circle $=2\sqrt{{{g}^{2}}-c}.............\left( iii \right)$
‘y’ intercept by the circle $=2\sqrt{{{f}^{2}}-c}...........\left( iv \right)$
Now, we can get values of g, f, c by comparing the equation (i) and standard equation of circle represented in equation (ii). So, we get
$g=\dfrac{-5}{2},f=0,c=-14$
Now, we can put values of g, f, c with the equation (iii) and (iv) to get the values of intercepts. Hence we get intercept on x-axis
$\begin{align}
  & =2\sqrt{{{\left( \dfrac{-5}{2} \right)}^{2}}-\left( -14 \right)} \\
 & =2\sqrt{\dfrac{25}{4}+4} \\
 & =2\sqrt{\dfrac{25+56}{4}}=2\sqrt{\dfrac{81}{4}} \\
 & =2\times \dfrac{9}{2}=9 \\
\end{align}$

So, the length of the intercept on the x-axis by the given circle is 9. Similarly we can get length of intercept on y-axis as intercept on y-axis
$\begin{align}
  & =2\sqrt{{{\left( 0 \right)}^{2}}-\left( -14 \right)} \\
 & =2\sqrt{0+4} \\
 & =2\sqrt{14} \\
\end{align}$
Hence, length of intercept on y-axis by the given circle is $2\sqrt{14}.$
Now, we can calculate the radius of the circle with the help of relation $\sqrt{{{g}^{2}}+{{f}^{2}}-c}$ as radius of given circle
$\begin{align}
  & =\sqrt{{{\left( \dfrac{-5}{2} \right)}^{2}}+{{\left( 0 \right)}^{2}}-\left( -14 \right)} \\
 & =\sqrt{\dfrac{25}{4}+14}=\sqrt{\dfrac{81}{4}} \\
 & =\dfrac{9}{2} \\
\end{align}$
Hence, the radius of the given circle is $\dfrac{9}{2}$ .
Now, we need to justify whether the given equation of conic will be a circle or not. General equation of conic is given as
$a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0..........\left( v \right)$
And it will represent a circle if $\Delta \ne 0,h=0,a=b$ where $\Delta $ can be given as
\[\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}.............\left( vi \right)\]
Now, compare the general equation of conic I equation (v) with the equation of circle given in equation (ii) and hence get
$a=1,h=0,b=1,g=\dfrac{-5}{2},f=0,c=-14$
Now, we can calculate values of $\Delta $ from the equation (vi) as
$\begin{align}
  & \Delta =\left( 1 \right)\left( 1 \right)\left( -14 \right)+2\times 0\times \left( \dfrac{-5}{2} \right)\times 0-1\times {{0}^{2}}-1{{\left( \dfrac{-5}{2} \right)}^{2}}-\left( -14 \right){{0}^{2}} \\
 & \Delta =-14-\dfrac{25}{4}=\dfrac{-81}{4}\ne 0 \\
\end{align}$
Hence, we can get the conditions of the circle that $\Delta \ne 0,a=b=1,h=0$ . Hence, the given equation is representing a circle. It’s justified now.

Note: One may use ${{\left( x-{{x}_{1}} \right)}^{2}}+{{\left( y-{{y}_{1}} \right)}^{2}}={{r}^{2}}$ as well in place of ${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$ where $\left( {{x}_{1}},{{y}_{1}} \right)$ is centre and r is radius.
$\begin{align}
  & {{x}^{2}}+{{y}^{2}}-5x-14=0 \\
 & \Rightarrow {{x}^{2}}-5x+{{y}^{2}}-14=0 \\
\end{align}$
Add ${{\left( \dfrac{5}{2} \right)}^{2}}$ and subtract it as well. So, we get
$\begin{align}
  & {{x}^{2}}-5x+{{\left( \dfrac{5}{2} \right)}^{2}}-{{\left( \dfrac{5}{2} \right)}^{2}}+{{y}^{2}}-14=0 \\
 & \Rightarrow {{x}^{2}}-2\times \dfrac{5}{2}\times x+{{\left( \dfrac{5}{2} \right)}^{2}}+{{y}^{2}}=14+{{\left( \dfrac{5}{2} \right)}^{2}} \\
 & {{\left( x-\dfrac{5}{2} \right)}^{2}}+{{y}^{2}}=14+\dfrac{25}{4}=\dfrac{81}{4} \\
 & \Rightarrow {{\left( x-\dfrac{5}{2} \right)}^{2}}+{{\left( y-0 \right)}^{2}}={{\left( \dfrac{9}{2} \right)}^{2}} \\
\end{align}$
So, centre is $\left( \dfrac{5}{2},0 \right)$ and radius is $\dfrac{9}{2}$
$\Delta =abc+2fgh-a{{f}^{2}}-b{{g}^{2}}-c{{h}^{2}}$
Can also be represented in determinant form as well. It is given as
$\Delta =\left| \begin{matrix}
   a & h & g \\
   h & b & f \\
   g & f & c \\
\end{matrix} \right|$
The intercept formulae
$2\sqrt{{{g}^{2}}-c},2\sqrt{{{f}^{2}}-c}$
Can be proved with the help of a standard form of circle as

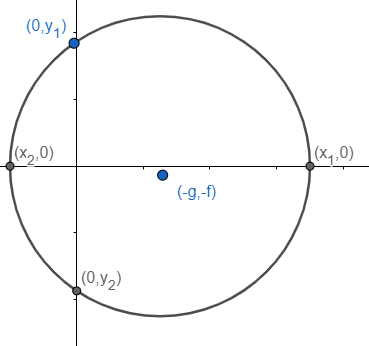
x-intercept = $\left| {{x}_{1}}-{{x}_{2}} \right|$ and y-intercept = $\left| {{y}_{1}}-{{y}_{2}} \right|$ as we have equation as
${{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0$
Put x = 0 and get quadratic in ‘y’ and hence calculate $\left| {{y}_{1}}-{{y}_{2}} \right|$ as ${{y}_{1}},{{y}_{2}}$ will be the roots of that quadratic. And similarly, put y = 0 to the standard equation and get quadratic in ‘x’ to calculate $\left| {{x}_{1}}-{{x}_{2}} \right|$ as ${{x}_{1}},{{x}_{2}}$ will be the roots of that quadratic.