Question

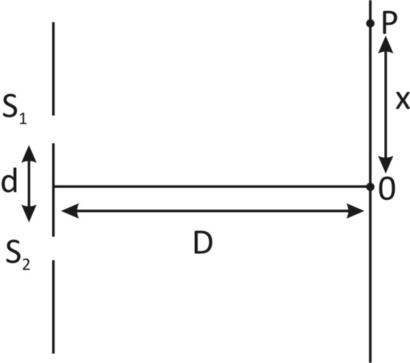
The intensity, at the central maxima (O) in a Young’s double slit set up is ${I_0}.$ If the distance OP equals one third of the fringe width of the pattern, show that the intensity, at point P, would equal \[{I_2}/4.\]

Answer 1

Hint: Concept of Young’s double slit experiment and the variation of intensity from central maximum to decreasing values as we go away from centre O. Also the lights entering from slits are from the same source , so the intensity at both slits are taken the same.

Formula used:
1. $\beta = \dfrac{{\lambda D}}{d}$
2. Path difference $ = \dfrac{{2\pi }}{\lambda } \times $phase differences
\[\varphi = \dfrac{{2\pi }}{\lambda } \times \]Path differences

Complete step by step answer:
In the question the intensity at central maxima is \[{I_{0.}}\] and we know that maximum intensity is given by
${\operatorname{I} _{max}} = {I_0} = {\left( {\sqrt {{I_1}} + \sqrt {{I_2}} } \right)^2}$Where ${I_1}$ and ${I_2}$respectively.
Here, ${I_1} = {I_2} = I$ (say)
So, maximum intensity becomes,
${I_0} = {\left( {\sqrt I + \sqrt I } \right)^2}$
${I_0} = {\left( {2\sqrt I } \right)^2}$
${I_0} = 4\,I\,\,.........\left( 1 \right)$
Now, intensity at point P which is at a distance of x from O us given by
\[{I_p} = \left( {{I_2} + {I_2} + 2\sqrt {{I_1}} \,\sqrt {{I_2}} \,\cos \phi } \right)\]
Where $\varphi $is the phase difference between two waves.
Since, ${I_1} = {I_2} = I$
So, \[{I_P} = \left( {I + {I_2} + 2\sqrt I \sqrt 1 \cos \phi } \right)\]
$ = \left( {2I + 2I\,\,\cos \phi } \right)$
$ = 2I\left( {I + \cos \phi } \right)$
$ = 2I \times 2{\cos ^2}\phi /2$ (as $I + \cos \phi = 2{\cos ^2}\dfrac{\phi }{2}$)
${I_P} = 4I\,\,{\cos ^2}\dfrac{\phi }{2}\,\,........\left( 2 \right)$
From (1) and (2), we have
\[{I_P} = {I_0}{\cos ^2}\dfrac{\phi }{2}\]
Now, according to question, distance OP us one-third of the fringe width i.e. $x = \dfrac{1}{3}\beta $
Where $\beta $ is fringe width
Now, we know that fringe width is given by $\beta = \dfrac{{\lambda D}}{\alpha }$
So, distance OP becomes,
$x = \dfrac{1}{3}\beta \,\, = \,\dfrac{1}{3} \times \dfrac{{\lambda D}}{d}$
$x = \dfrac{{\lambda D}}{{3d}}$ and we know that path difference and phase difference are related as $2\pi \times $phase difference $ = \alpha \times $path difference
\[ \Rightarrow d = \dfrac{{2\pi }}{\lambda } \times \dfrac{{xd}}{D}\]
\[ \Rightarrow d = \dfrac{{2\pi }}{\lambda } \times \dfrac{{\lambda D}}{{3d}} \times \dfrac{d}{D}\]
$ \Rightarrow \phi = \dfrac{{2\pi }}{3}........\left( 3 \right)$
Put equation $\left( 3 \right)$ in equation$\left( 2 \right)$, we get
$I = {I_0}{\cos ^2}\left( {\dfrac{{2\pi }}{{\dfrac{3}{2}}}} \right)$
\[I = {I_0}{\cos ^2}\left( {\dfrac{\pi }{3}} \right)\]
$I = {I_0}{\left( {\dfrac{1}{2}} \right)^2}$
\[I = \dfrac{{{I_0}}}{4}\]
Hence Proved.

Note:
Remember that for the same source ${I_1} = {I_2}$and for different sources ${I_1} \ne {I_2}$ and the also remember that with change in path length there is corresponding change in phase also.