Question

The incircle of an isosceles triangle ABC, In which AB = AC, touches the sides BC, CA, and AB at Q, R, and P respectively. Prove that BQ = QC.

Answer 1

Hint: Start by drawing a neat diagram followed by using the theorem that the tangents to a circle from a given point outside the circle are equal.

Complete step-by-step answer:
First, we will draw a neat diagram of the situation given in the question.

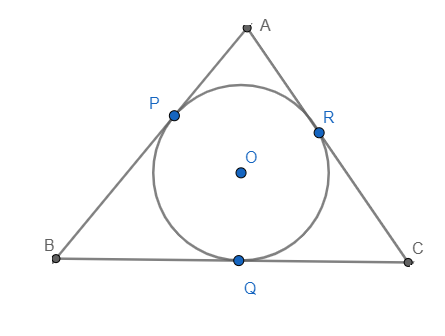
We know that the tangents drawn from a given point to the circle are equal. And it is clear from the figure that AP and AR are tangents drawn from point A, BP, and BC are tangents from point B, and CQ and CR are tangents from point C.
$\therefore AP=AR.............(i)$
$\therefore BP=BQ...........(ii)$
$\therefore CR=CQ...........(iii)$
Now, as it is mentioned in the question, that $\Delta ABC$ is an isosceles triangle.
$\therefore AB=AC$
Using the diagram, we can write AB as the sum of AP and BP, and AC as the sum of AR and CR.
$AP+BP=AR+CR$
Now substituting the value of AP from equation (i), BP from equation (ii), and CR from equation (iii), we get
$\Rightarrow AR+BQ=AR+CQ$
 $\Rightarrow BQ=CQ$
Hence we have proved that BQ = CQ as asked in the question.

Note: The centre of the largest circle that fits inside a triangle is called the incentre and is defined as the meeting point of all three angle bisectors of the triangle. In the above figure, O is the incentre of the $\Delta ABC$ . Always draw a neat diagram before starting problems related to geometry, as it’s easy to visualise a question with a diagram in front of us.