Question

The image of $P\left( {a,b} \right)$ in the line $y = - x$ is $Q$ and the image of $Q$ in a line $y = x$ is $R$. Then the midpoint of $PR$ is:
A. $\left( {a + b,b + a} \right)$
B. $\left( {\dfrac{{a + b}}{2},\dfrac{{b + a}}{2}} \right)$
C. $\left( {a - b,b - a} \right)$
D. $\left( {0,0} \right)$

Answer 1

Hint: In the given question first we will make the diagram, then according to the question find the line equation which is perpendicular to $y = - x$and passes through $\left( {a,b} \right)$ using the formula$\dfrac{{y - {y_1}}}{{x - {x_1}}} = 1$, thus we will get the line equation and consider it as equation $1$ , given that the point where it intersects is $y = - x$ put this in equation $1$ we will get the value of $x$ and similarly for $y$. Now we get the points$Q\& R$. After that we will apply the formula $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$and find the points of$PR$. Thus we will get the desired answer.

Complete step by step Answer:

Consider the diagram according to the question:

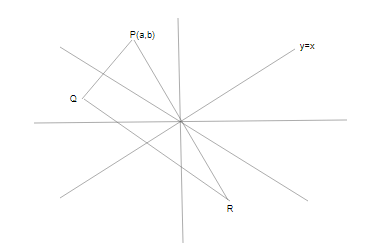
First, we consider the point $P\& Q$
The line which is perpendicular to $y = - x$and passes through $\left( {a,b} \right)$ will be
$\dfrac{{y - {y_1}}}{{x - {x_1}}} = 1$
$\dfrac{{y - b}}{{x - a}} = 1$
$y = x - \left( {a - b} \right)..........\left( 1 \right)$
Now the point where it intersects is $y = - x$is
$
   - x = x - \left( {a - b} \right) \\
  2x = \left( {a - b} \right) \\
  x = \dfrac{{a - b}}{2} \\
 $
Put the value of $x$ in equation $1$
Hence we can say that
$
  y = x - \left( {a - b} \right) \\
   \Rightarrow y = \dfrac{{a - b}}{2} - \left( {a - b} \right) \\
   \Rightarrow y = \dfrac{{a - b - 2\left( {a - b} \right)}}{2} \\
   \Rightarrow y = \dfrac{{a - b - 2a + 2b}}{2} \\
   \Rightarrow y = \dfrac{{b - a}}{2} \\
 $
This will be the midpoint of $PQ$ since $Q$ is the image of point P on the line $y = - x$
Therefore
$Q = \left( { - b, - a} \right)$
And similarly
$R = \left( { - a, - b} \right)$
Now the points of $PR$ are:
 $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)............\left( 2 \right)$
Where
$P\left( {a,b} \right)$
And
$R = \left( { - a, - b} \right)$
Now put this value in equation 2
$
  {x_1} = a,{y_1} = b \\
  {x_2} = \left( { - a} \right),{y_2} = \left( { - b} \right) \\
$
Now
$
  P\& R = \left( {\dfrac{{a + \left( { - a} \right)}}{2},\dfrac{{b + \left( { - b} \right)}}{2}} \right) \\
   \Rightarrow \left( {0,0} \right) \\
 $
Hence the midpoint of $PR$ will be $\left( {0,0} \right)$
Thus the correct answer is option D

Note: First of all we draw the diagram according to the question, then by using the formula $\dfrac{{y - {y_1}}}{{x - {x_1}}} = 1$find the value of$x,y$. We have to remember this formula. Thus we get the points of $Q\& R$ and $P$ point is already given in the question. We have to remember one more formula i.e. $\left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$to find the points of$P,R$. Hence we get the correct answer.