Question

The height of the hollow cylinder is 10 cm. What is the volume and surface area of a hollow cylinder with inner radius 3 cm and outer radius 6 cm? (Use$\pi = 3$).

Answer 1

Hint – We will solve this question by noting down all the given information in the question and by using this information we will draw a figure to make it easier for us. By using the formula of the Volume of the hollow cylinder and the Surface Area of the hollow cylinder, we will get our solutions.

Complete step-by-step answer:

It is mentioned in the question that the height of the hollow cylinder is 10 cm and its inner and outer radii are 3 cm and 6 cm, respectively.
So, according to this, our figure must look like this,

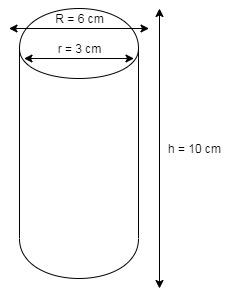
Given that,
Height of the hollow cylinder$\left( h \right)$ = 10 cm
Inner radius of the hollow cylinder $\left( r \right)$ = 3 cm
And, outer radius of the hollow cylinder $\left( R \right)$ = 6 cm
Now, we know that the formula of the Volume of the cylinder is $\pi {r^2}h$, but here we have a hollow cylinder with two radii, i.e., inner radius and outer radius, therefore the formula becomes,

Volume of the hollow cylinder $ = \pi h\left( {{R^2} - {r^2}} \right)$
                                                       $
   = \pi \times 10\left( {{6^2} - {3^2}} \right) \\
   = \pi \times 10\left( {36 - 9} \right) \\
   = \pi \times 10\left( {27} \right) \\
   = \pi \times 270 \\
   = 3 \times 270 \\
   = 810c{m^3} \\
 $
Hence, Volume of the cylinder is $810c{m^3}$ .

Also, we know that the formula of the Surface Area of the cylinder is $2\pi rh + 2\pi {r^2}$, but here we have a hollow cylinder with two radii, i.e., inner radius and outer radius, therefore the formula becomes,

Surface area of the hollow cylinder $ = 2\pi rh + 2\pi Rh + 2\left( {\pi {R^2} - \pi {r^2}} \right)$
                                                                $
   = 2\pi \times 3 \times 10 + 2\pi \times 6 \times 10 + 2\left( {\pi {6^2} - \pi {3^2}} \right) \\
   = 2\pi \left( {30 + 60} \right) + 2\left[ {\pi \left( {36 - 9} \right)} \right] \\
   = 2\pi \left( {90} \right) + 2\left( {27\pi } \right) \\
   = 2 \times 3\left( {90} \right) + 2\left( {27 \times 3} \right) \\
   = 6\left( {90} \right) + 2\left( {81} \right) \\
   = 540 + 162 \\
   = 702c{m^2} \\
 $
Hence, Surface Area of the hollow cylinder is $702c{m^2}$.
Note - A Cylinder is a closed solid that has two parallel bases joined by a curved surface, at a fixed distance. While solving these kinds of questions, one should not have any doubts related to the formula because we have used different formulas which might be confusing sometimes.