Question

The height of the chimney when it is found on walking towards it 50 meters in the horizontal line through its base, the angle of elevation top changes from ${30^0}$ to ${60^0}$ is
A) $25\sqrt 3 {\text{ m}}$
B) $25{\text{ m}}$
C) $25\sqrt 4 {\text{ m}}$
D) $\dfrac{{25}}{{\sqrt 3 }}{\text{ m}}$

Answer 1

Hint:
In this question, we need to determine the height of the chimney such that the angle of elevation from two different points on the collinear points with the ground has been given. For this, we will use the tangent of the trigonometric functions to establish a relation between the height of the tower and the length of the point from the foot of the tower.

Complete step by step solution:
Let us consider a chimney of height OT with the top point at T.

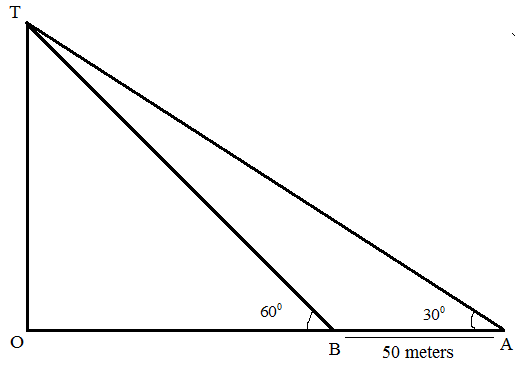
The ratio of the perpendicular and the base of the right-angled triangle is the trigonometric tangent of the triangle. Mathematically, $\tan \theta = \dfrac{{perpendicular}}{{base}}$.
In the triangle TOA, angle TOA is at right-angle, and so, AT acts as the hypotenuse of the triangle, TO as the perpendicular, and OA as the base for the angle TAO.
According to the question, $\angle TAO = {30^0}$. So, substituting the same in the formula, $\tan \theta = \dfrac{{perpendicular}}{{base}}$ we get
$
  \tan \theta = \dfrac{{perpendicular}}{{base}} \\
   \Rightarrow \tan \left( {\angle TAO} \right) = \dfrac{{OT}}{{OA}} \\
   \Rightarrow \tan {30^0} = \dfrac{{OT}}{{OB + BA}} \\
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{{OT}}{{OB + 50}} \\
   \Rightarrow OT = \dfrac{{OB + 50}}{{\sqrt 3 }} - - - - (i) \\
 $
Again, In the triangle TOB, angle TOB is at right-angle, and so, TB acts as the hypotenuse of the triangle, TO as the perpendicular, and OB as the base for the angle TBO.
According to the question, $\angle TBO = {60^0}$. So, substituting the same in the formula, $\tan \theta = \dfrac{{perpendicular}}{{base}}$ we get
$
  \tan \theta = \dfrac{{perpendicular}}{{base}} \\
   \Rightarrow \tan \left( {\angle TBO} \right) = \dfrac{{OT}}{{OB}} \\
   \Rightarrow \tan {60^0} = \dfrac{{OT}}{{OB}} \\
   \Rightarrow \sqrt 3 = \dfrac{{OT}}{{OB}} \\
   \Rightarrow OB = \dfrac{{OT}}{{\sqrt 3 }} - - - - (ii) \\
 $
Substituting the values from equation (ii) in the equation (i), we get
$
  OT = \dfrac{{OB + 50}}{{\sqrt 3 }} \\
   \Rightarrow OT = \dfrac{{\left( {\dfrac{{OT}}{{\sqrt 3 }}} \right) + 50}}{{\sqrt 3 }} \\
   \Rightarrow \sqrt 3 OT - \left( {\dfrac{{OT}}{{\sqrt 3 }}} \right) = 50 \\
   \Rightarrow OT\left( {\sqrt 3 - \dfrac{1}{{\sqrt 3 }}} \right) = 50 \\
   \Rightarrow OT\left( {\dfrac{{3 - 1}}{{\sqrt 3 }}} \right) = 50 \\
   \Rightarrow OT = \dfrac{{50\sqrt 3 }}{2} \\
   \Rightarrow OT = 25\sqrt 3 {\text{ meters}} \\
 $
Hence, the height of the chimney is $25\sqrt 3 {\text{ meters}}$.

Hence, Option A is correct.

Note:
It is interesting to note here that whenever the horizontal distance (or the foot distance) between the objects is less then, the angle subtended between them will be high. Here, as the boy travelled a distance of 50 meters towards the chimney then the angle of elevation of the top of the chimney with respect to the boy increases from 30 to 60 degrees.