Question

The gravitational field in a region is given by equation\[E=(5i+12j){N}/{kg}\;\]. If the particle of mass 2 kg is moved from the origin to the point (12m, 5m) in this region, the change in gravitational potential energy is:
A. -225 J
B. -240 J
C. -245 J
D. -250 J

Answer 1

Hint: The given question is based on the concept of the relation between the electric field and the potential. Thus, we will make use of the formula that relates the parameters such as, the electric field, the potential and the distance (radius) to find the value of the potential difference. Then, we will multiply the obtained value with the mass to obtain the value of the change in gravitational potential energy.
Formulae used:
\[E=-\dfrac{dV}{dr}\]
\[dU=m\times dV\]

Complete answer:
The formula that relates the parameters such as, the electric field, the potential and the distance (radius) is given as follows.
\[E=-\dfrac{dV}{dr}\]
Where E is the electric field, dV is the change in the potential value and dr is the change in the distance.
From the data, we have the data as follows.
The gravitational field value, \[E=(5i+12j){N}/{kg}\;\].
The distance at origin, \[{{r}_{o}}=(0,0)\]
The distance at some point, \[{{r}_{f}}=(12m,5m)\]
The mass of the particle, m = 2 kg

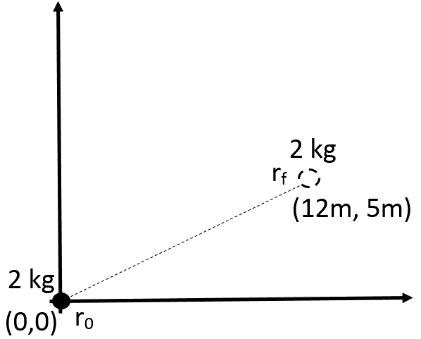
Firstly, we will compute the change in the distance of the particle. So, we have,
\[dr={{r}_{f}}-{{r}_{o}}\]
Now, substitute the given values in the above equation.
\[\begin{align}
  & dr=(12m,5m)-(0,0) \\
 & dr=(12-0)i+(5-0)j \\
\end{align}\]
The vector representation of the change in the distance of the particle is given as follows.
\[dr=12i+5j\]
Now, substitute the values of the field and the distance to obtain the value of the potential. So, we get,
\[\begin{align}
  & dV=-E.dr \\
 & dV=-[(5i+12j).(12i+5j)] \\
\end{align}\]
The dot product is calculated as follows.
\[\begin{align}
  & dV=-[(5\times 12)i+(12\times 5)j] \\
 & dV=-(60+60) \\
 & \Rightarrow dV=-120 \\
\end{align}\]
The change in gravitational potential energy is calculated as follows.
\[dU=m\times dV\]
Substitute the values.
\[\begin{align}
  & dU=2\times -120 \\
 & dU=-240\,J \\
\end{align}\]
\[\therefore \] The change in gravitational potential energy is – 240 J

As, the value of the change in gravitational potential energy is – 240 J, thus, the option (B) is correct.

Note:
This is a direct theoretical question. The important step to remember while calculating such a problem is the calculation of the change in gravitational potential energy using the value of the potential difference and the mass. The units of the parameters should be taken care of, as, in this case, the distance is given in terms of meters and the unit of the mass is given in terms of kg, so, no need to change.