Question

The graph of \[x = 8\] represents:
A. Line parallel to \[y\]–axis and at a distance of 8 units.
B. Line parallel to \[x\]–axis and at a distance of 8 units.
C. Line parallel to \[y\]–axis and at a distance of 0 units.
D. None of these

Answer 1

Hint: First we will compare the given equation with the graph of the standard equation \[x = k\] is a line parallel to \[y\]–axis at a distance of \[k\] units and passing through the point \[\left( {k,0} \right)\] to find the value of \[k\] and then we will compare the obtained statement with the options to find the correct option.

Complete step by step answer:

We are given that equation
 \[x = 8{\text{ ......eq.(1)}}\]

We know that the graph of the standard equation \[x = k\] is a line parallel to \[y\]–axis at a distance of \[k\] units and passing through the point \[\left( {k,0} \right)\].

Comparing the above standard equation with the equation (1) to find the value of \[k\], we get
 \[ \Rightarrow k = 8\]

Thus, we have that the graph of \[x = 8\] is a line parallel to \[y\]–axis at a distance of 8 units and passing through the point \[\left( {8,0} \right)\].

Graphing the equation (1), which passes through the point \[\left( {8,0} \right)\], we get

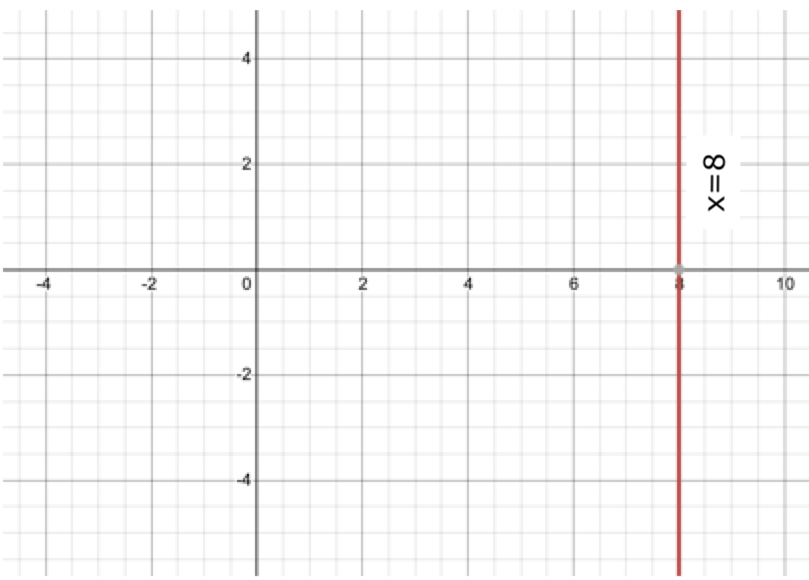
Thus, we have the graph of equation (1) represents a line parallel to \[y\]–axis and at a distance of 8 units.
Hence, option A is correct.

Note: In solving these types of questions, you need to know that the basic properties and meaning of the equation of the vertical and horizontal line. One should know that to locate a line on a graph, we will locate the \[y\]– intercept on the graph and then plot the point. When a line is vertical, then no matter which value of \[y\] is used.