Question

The graph of the quadratic polynomial; y = $ a{{x}^{2}} $ + bx + c is as shown in the figure. Then:

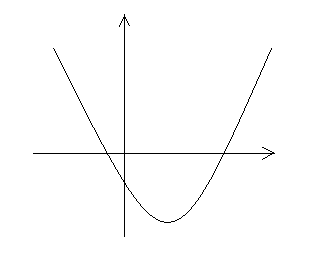
A. $ {{b}^{2}} $ − 4ac > 0
B. b > 0
C. a < 0
D. All of these.

Answer 1

Hint: Observe that the parabola is opening upwards which means that the values of y are increasing in the positive direction. What does it tell about the coefficient a of the term $ a{{x}^{2}} $ ?
Locate the position of the roots of the parabola. Are real roots real or imaginary (no real roots)? What does it tell about the value of the discriminant $ {{b}^{2}} $ − 4ac?

Complete step-by-step answer:
It should be observed that the value of $ {{x}^{2}} $ is always positive and greater than the terms bx and c for large magnitudes of x. Therefore, the sign of the multiplier a in the term $ a{{x}^{2}} $ , decides whether the value of y will move in the positive or negative direction for an increase in the magnitude of x in either direction. This is illustrated in the following graphs:

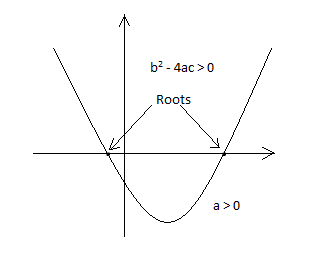
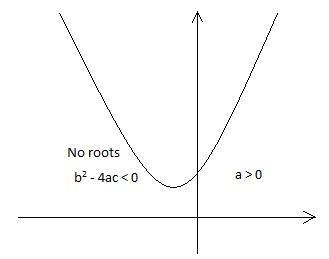
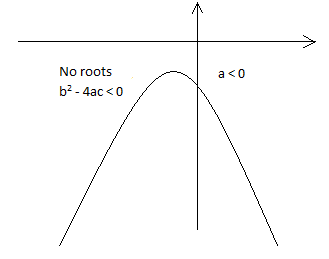
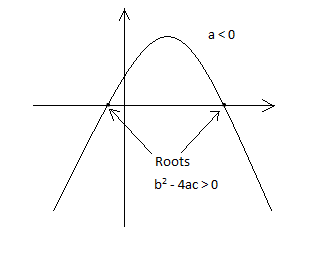
Since the given graph has two real roots and it opens upwards in the positive direction, we can conclude that a > 0 and $ {{b}^{2}} $ − 4ac > 0 (see Note below).
The correct answer is A. $ {{b}^{2}} $ − 4ac > 0.

Note: The roots (also called as zeros, y = 0) of the quadratic equation $ a{{x}^{2}} $ + bx + c = 0 are given by x = $ \dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a} $ . The quantity $ {{b}^{2}} $ − 4ac is called the discriminant of the equation and determines the nature of its roots.
If $ {{b}^{2}} $ − 4ac ≥ 0, the roots are real.
If $ {{b}^{2}} $ − 4ac = 0, the roots are real and equal.
If $ {{b}^{2}} $ − 4ac < 0, the roots are complex and conjugates of each other.