Question

The graph of $f(x)=10-4{{e}^{-2x}}$ is shown. What is the area of triangle ABC if OA = AB?

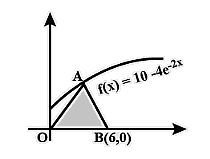
Answer 1

Hint:
1) The vertex of an isosceles triangle is always at the center with respect to its opposite side.
2) Area of a triangle is given by $\dfrac{1}{2}\times b\times h$, where b is the length of a side taken as the base and h is the height of the vertex opposite to this side (base).
3) On an x-y plane, a point represented by P (a, b) means that the horizontal distance of P from the y-axis is a and the vertical distance of P from the x-axis is b.
4) For a point P (a, b), a is the value of x and b is the value of y.
5) If a point (a, b) lies on a given function y = f(x), then b = f(a).

Complete step by step solution:
Let’s say that the point A is (a, b).

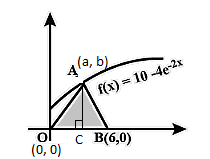
OB = Horizontal distance = Difference in the values of x of points O and B = 6 - 0 = 6 units.
Since, in Δ AOB, AO = AB (given), therefore, A must be at the middle with respect to line OB.
∴ A must be at a distance of $\dfrac{6}{2}=3$ units from the y-axis, which also means that the value of a for the point A (a, b) is 3. We can now write point A as (3, b).
Now, since A (3, b) is also on the graph of the curve $f(x)=10-4{{e}^{-2x}}$ , therefore we must have:
 $b=f(3)=10-4{{e}^{-2\times 3}}=10-\dfrac{4}{{{e}^{6}}}$ units. This is the vertical distance of the point A from the x-axis.
Now, in Δ AOB, if we consider OB as the base, then AC will be the height which is the vertical distance of the point A (a, b) from the x-axis, i.e. $AC=b=10-\dfrac{4}{{{e}^{6}}}$ .
∴ The area of Δ AOB = \[\dfrac{1}{2}\times OB\times AC=\dfrac{1}{2}\times 3\times \left( 10-\dfrac{4}{{{e}^{6}}} \right)=15-\dfrac{6}{{{e}^{6}}}\approx 15-0.0148\approx 14.98\] sq. units.

Note:
1) Any side of a triangle can be chosen as the base and the height corresponding to the chosen base only must be considered while calculating the area.
2) The number ‘e’ is the Euler’s constant and its value is approximately 2.7182…