Question

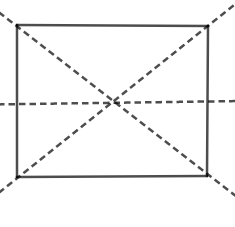
The given figure has more than one line of symmetry. Such figures are said to have multiple lines of symmetry. Identify multiple lines of symmetry, if any in the given figure.

Answer 1

Hint: Line of symmetry is a line along which if we fold the figure then the two parts generated after making a line will coincide with each other and it is given that the figure has multiple lines of symmetries. From the definition of line of symmetry we can see that there are three lines of symmetry given in the question.

Complete step-by-step answer:
In the below figure, we have labeled the figure given in the question as ABCD and MN.

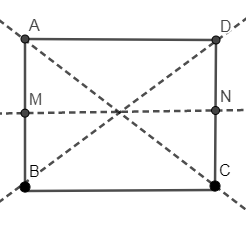
In the above figure, we can see a square ABCD and three dotted lines passing through AC, BD and MN.
We are saying the three dotted lines as the line of symmetries because if we fold the figure along each line of symmetry then the two parts that were generated due to the line of symmetry will coincide with each other. For e.g., if we fold the square ABCD along BD then $\Delta BAD$ will coincide with $\Delta BCD$ so we can say that BD is the line of symmetry. Similarly, we can prove the other line of symmetries.
Hence, we have identified three lines of symmetries AC, BD and MN in the given figure.

Note: We can redefine the definition of line of symmetry as it is a line which divides the whole figure in two equal parts.
If a figure has a line of symmetry then it divides the figure in two parts in such a way that one of the parts of the divided figure is the reflection of the other part of the divided figure and the line of symmetry is acting as a mirror in which the reflection has occurred.

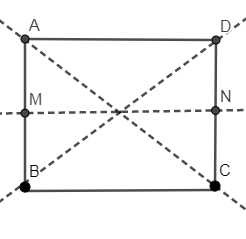
The above definition of line of symmetry, we can check through an example. In the above figure, BD is acting as a mirror and BCD is the reflection of BAD. Similarly, you can verify yourself for other lines of symmetries too.