Question

The given figure depicts a racing track whose left and right ends are semicircular. The distance between the two inner parallel line segments is 60m and they are each 106m long. If the track is 10m wide, find:
(i) The distance around the track along its inner edge.
(ii) The area of the track.

Answer 1

Hint: In order to find the distance around the track along the inner edge and the area, we make use of the concepts of area of a rectangle, area and circumference of a semicircle. We construct a new figure with appropriate notations using the given data and the given figure to help us find the answer easily.

Formula Used
Area of a rectangle = l × b
Circumference of a semicircle = πr
Area of a semicircle = \[\dfrac{{\pi {{\text{r}}^2}}}{2}\]

Complete step-by-step answer:
We draw a new figure with the given data and we name it according to our choice for our convenience, to help us solve the problem easily, it is as follows:

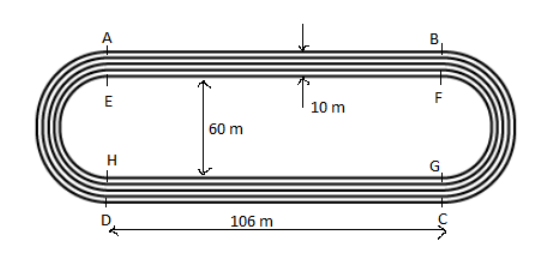
The distance around the track along its inner edge:
From the figure we can express the distance around the tract along its inner edge as,
D = EF + HG + circumference of semicircle with diameter EH + circumference of semicircle with diameter FG.
We know, circumference of a semicircle = πr.
EH = FG = diameter of the semicircle’s respectively.
Given EH = FG = 60 m, therefore radius r = 30 m respectively.
And from the figure EF = HG = 106 m
Therefore D = 30π + 30π + 106 + 106
Take π =$\dfrac{{22}}{7}$, we get the distance around the tract along its inner edge =$\dfrac{{2804}}{7}$m.

Area of the track:
From the figure, area of the track can be expressed as,
A = Area of rectangle ABFE + Area of rectangle HGCD + (Area of semicircle with diameter AD – Area of semicircle with diameter EH) + (Area of semicircle with diameter BC – Area of semicircle with diameter FG)
We know, Area of a rectangle = l × b
Area of a semicircle = \[\dfrac{{\pi {{\text{r}}^2}}}{2}\]
From the figure, AB = HG = 106 m
AE = HD = 10 m
AD = BC = 60 + 10 + 10 = 80 m
AD and BC are the diameters of the two outer semicircles, hence their individual radius is equal to$\dfrac{{80}}{2}$= 40 m.
EH = FG = 60 m
EH and FG are the diameters of the two inner semicircles, hence their individual radius is equal to$\dfrac{{60}}{2}$= 30 m.
Therefore A =$\left( {106 \times 10} \right) + \left( {106 \times 10} \right) + \left( {\dfrac{\pi }{2} \times 40 \times 40 - \dfrac{\pi }{2} \times 30 \times 30} \right) + \left( {\dfrac{\pi }{2} \times 40 \times 40 - \dfrac{\pi }{2} \times 30 \times 30} \right)$
A = 2120 + 2200 = 4320 sq m.
The area of the track is 4320${{\text{m}}^2}$.

Note: In order to solve this type of problem the key is to construct a proper diagram depicting all the data given in the question and naming it accordingly so that we can split the quantity to be found out. We split it in a way that they form smaller geometrical figures for which the area or circumference can be determined using the formula we already know.
The diameter of a circle or a semicircle is two times its radius, given by d = 2r.
Area is always calculated in square units. 1 square meter can also be written as 1${{\text{m}}^{\text{2}}}$.