Question

The function $f\left( x \right) = \left| {px - q} \right| + r\left| x \right|{\text{ , }}x \in \left( { - \infty ,\infty } \right)$ where $p \succ 0,{\text{ q}} \succ {\text{0, r}} \succ {\text{0}}$ assumes its minimum value only at one point if;
$\left( 1 \right)p \ne q$
$\left( 2 \right)q \ne r$
$\left( 3 \right)r \ne p$
$\left( 4 \right)p = q = r$

Answer 1

Hint: To solve this question, we should be familiar with the definition of modulus function. A modulus function or absolute value function gives the absolute value of a number or a variable. The output of a modulus function is always positive whatever the input is; it is represented as $y = \left| x \right|$ , ${\text{where }}x \in R$ .
The definition of a modulus function is given by, $\left| x \right| = \left\{ \begin{gathered}
  x,{\text{ if }}x \geqslant 0 \\
   - x,{\text{ if }}x \prec 0{\text{ }} \\
\end{gathered} \right.$.

Complete step-by-step solution:
Using the above definition of modulus function, we can expand $\left| {px - q} \right|$ ;
$ \Rightarrow \left| {px - q} \right| = 0$
We get the value of $x$ as;
$ \Rightarrow x = \dfrac{q}{p}$
\[ \Rightarrow \left| {px - q} \right| = \left\{ \begin{gathered}
  px - q{\text{ if }}x \geqslant \dfrac{q}{p} \\
   - \left( {px - q} \right){\text{ if }}x \prec \dfrac{q}{p} \\
\end{gathered} \right.\]
Now, we can define our function in three regions;

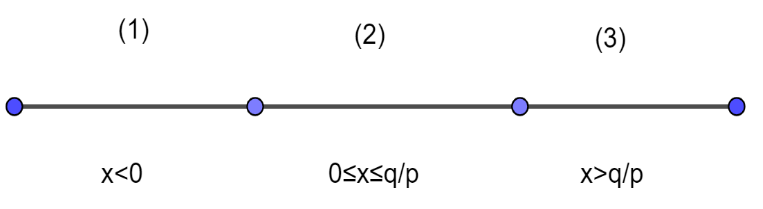
Figure $1$ : The function in three different regions
According to figure $\left( 1 \right)$ , we can define our function as;
$ \Rightarrow f\left( x \right) = \left| {px - q} \right| = \left\{ \begin{gathered}
   - \left( {px - q} \right) - rx{\text{ }}x \leqslant 0 \\
   - \left( {px - q} \right) + rx{\text{ }}0 \leqslant x \leqslant \dfrac{q}{p} \\
  px - q + rx{\text{ }}x \succ \dfrac{q}{p} \\
\end{gathered} \right.$
On simplifying further, we get;
$ \Rightarrow f\left( x \right) = \left| {px - q} \right| = \left\{ \begin{gathered}
  q - \left( {p + r} \right)x{\text{ }}x \leqslant 0 \\
  q + \left( {r - p} \right)x{\text{ }}0 \leqslant x \leqslant \dfrac{q}{p} \\
   - q + \left( {p + r} \right)x{\text{ }}x \succ \dfrac{q}{p} \\
\end{gathered} \right.$
According to the question, we know that $p \succ 0,{\text{ q}} \succ {\text{0, r}} \succ {\text{0}}$ , so we can say that $p + r \succ 0$ therefore the term $q - \left( {p + r} \right)x{\text{ }}$ will have a negative slope, and also the term $ - q + \left( {p + r} \right)x{\text{ }}$, will also have a positive slope. But we can not predict anything about slope of $q + \left( {r - p} \right)x{\text{ }}$ in the interval $0 \leqslant x \leqslant \dfrac{q}{p}$ . So, let us analyze this term for three different conditions;

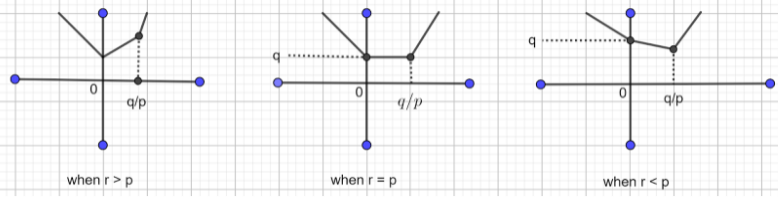
Figure $\left( 2 \right)$ : Analyzing the function $ - q + \left( {p + r} \right)x{\text{ }}$ for three different regions
Notice that in figure $\left( 2 \right)$ in the first case when ( $r \succ p$ ) we get the minimum value $q$ for the function at point $x = 0$ . In the third case also $r \prec p$ we get the minimum value at $x = \dfrac{q}{p}$ . But in the second case when $\left( {r = p} \right)$ , we have the same minimum value between $0{\text{ and }}\dfrac{p}{q}$ as the function constantly gives the same value as $q$ ( means infinite minimum points ) and in the question they have asked the minimum value at only one point, hence we do not want this case . Therefore, according to the question the function $\left| {px - q} \right|$ assumes its minimum value when $r \ne p$ as we have analyzed above.
Therefore, the correct answer for this question is option $\left( 3 \right)$ i.e. $r \ne p$ .

Note: We should have knowledge about how to predict the behavior of function as minimum and maximum. The maximum value is the highest point or value that the function can reach in a graph, it is also called as global maxima (the highest peak) while the other peaks in the graph are termed as local maxima. The same concept applies for the minimum value as well , the lowest value of a function for a graph is called the global minima ( the lowest point) of that function , while the other lower valleys are called local minima.