Question

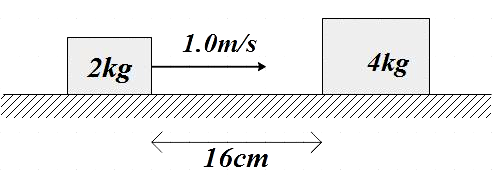
The friction coefficient between the horizontal surface and each of the blocks shown in the figure is 0.2. The collision between the blocks is perfectly elastic. Find the separation (in cm) between them when they come to rest. Take $g=10m{{s}^{-2}}$.

Answer 1

Hint: Firstly apply work energy theorem to find velocity of 2kg block just before collision. Now applying the law of conservation of kinetic energy and momentum, we get two equations in terms of velocities of the blocks after collision. Then, you could find the distance travelled by each block after collision before it goes to rest by solving the above relations and applying work energy theorem for each block, sum of which gives you the required separation.

Formula used:
Work energy theorem,
$\Delta K.E=W$
Law of conservation of momentum,
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Law of conservation of kinetic energy,
$\dfrac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{u}_{2}}^{2}=\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$

Complete answer:
In the question, we are given the coefficient of friction as 0.2 and acceleration due to gravity as $10m{{s}^{-2}}$
From the work energy theorem we know that the changing kinetic energy of a body will give us the work done on the body to move the body over a given distance.
Let $u$ be the initial velocity of the body, ${{u}_{1}}$ be the velocity of the body just before collision, the distance covered before collision is given as $S=16cm=0.16m$ and the work done is against the frictional force, so the force here is given by,
${{F}_{f}}={{\mu }_{s}}mg=0.2\left( 2\times 10 \right)=4N$
By work energy theorem,
$\Delta K.E=W$
$\Rightarrow \dfrac{1}{2}m{{u}_{1}}^{2}-\dfrac{1}{2}m{{u}^{2}}=W={{F}_{f}}\times S$
$\Rightarrow \dfrac{1}{2}\times 2\times {{u}_{1}}^{2}-\dfrac{1}{2}\times 2\times {{1}^{2}}=4N\times 0.16m$
$\Rightarrow {{u}_{1}}^{2}=1-0.64=0.36$
$\Rightarrow {{u}_{1}}=0.6m{{s}^{-1}}$ ……………………………. (1)
Let ${{u}_{1}}$ and ${{u}_{2}}$ be the velocities of bodies before collision and ${{v}_{1}}$ and ${{v}_{2}}$ be the velocities after it. Then by the law of conservation of momentum we have,
${{m}_{1}}{{u}_{1}}+{{m}_{2}}{{u}_{2}}={{m}_{1}}{{v}_{1}}+{{m}_{2}}{{v}_{2}}$
Second body is at rest initially, ${{u}_{2}}=0$
Substituting (1),
$\Rightarrow 2\left( 0.6 \right)+0=2{{v}_{1}}+4{{v}_{2}}$
$\Rightarrow {{v}_{1}}=0.6-2{{v}_{2}}$ ………………………………. (2)
As the collision is elastic, the kinetic energy is also conserved, therefore,
$\dfrac{1}{2}{{m}_{1}}{{u}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{u}_{2}}^{2}=\dfrac{1}{2}{{m}_{1}}{{v}_{1}}^{2}+\dfrac{1}{2}{{m}_{2}}{{v}_{2}}^{2}$
$\Rightarrow \dfrac{1}{2}\times 2{{\left( 0.6 \right)}^{2}}+0=\dfrac{1}{2}\times 2{{v}_{1}}^{2}+\dfrac{1}{2}\times 4{{v}_{2}}^{2}$
$\Rightarrow {{v}_{1}}^{2}+2{{v}_{2}}^{2}=0.36$
Substituting (2),
$\Rightarrow {{\left( 0.6-2{{v}_{2}} \right)}^{2}}+2{{v}_{2}}^{2}=0.36$
$\Rightarrow 0.36+4{{v}_{2}}^{2}-2.4{{v}_{2}}+2{{v}_{2}}^{2}=0.36$
$\Rightarrow 6{{v}_{2}}^{2}=2.4{{v}_{2}}$
$\Rightarrow {{v}_{2}}=0.4m{{s}^{-1}}$ ………………………. (3)
From (2),
${{v}_{1}}=0.6-2\left( 0.4 \right)=-0.2m{{s}^{-1}}$ …………………………. (4)
After collision 2kg block and 4kg block cover distances ${{x}_{1}}$ and ${{x}_{2}}$ respectively from the point collision and then go to rest. Applying work energy theorem for both cases, we get,
For 2kg block,
$\dfrac{1}{2}\left( 2 \right){{\left( {{v}_{1}} \right)}^{2}}={{F}_{s}}{{x}_{1}}$
$\Rightarrow \dfrac{1}{2}\left( 2 \right){{\left( 0.2 \right)}^{2}}=4{{x}_{1}}$
$\Rightarrow {{x}_{1}}=0.01m=1cm$ …………………………………. (5)
For 4kg block,
$\dfrac{1}{2}\left( 4 \right){{\left( {{v}_{2}} \right)}^{2}}={{F}_{s}}{{x}_{2}}$
$\Rightarrow \dfrac{1}{2}\left( 4 \right){{\left( 0.4 \right)}^{2}}=4{{x}_{2}}$
$\Rightarrow {{x}_{2}}=0.04m=4cm$………………………………….. (6)
From (3) and (4) we know that both bodies after collision move in opposite directions, so, distance of separation must be given by the sum of (5) and (6).

Note:
From (3) and (4), where we had found the velocities of the blocks after collision, we see that they both are directed opposite to each other. And using this fact we have calculated the distance of separation. Also, while applying the work energy theorem in the last part where we found the distance covered by each body after collision, we have taken the final K.E zero as the distance is calculated when the body is at rest.