Question

The frame of brass plate of an outer door design has area 1.60$m^2$ and thickness 1 cm. The brass plate experiences shear force due to earthquake. How large a parallel force must be exerted on each of its edges, if the lateral displacement is 0.32 mm?

Answer 1

Hint: The shear force acts along the back and front of the brass plate and causes a displacement in the bottom part so that one face is displaced by 0.32 mm with respect to another face of the brass plate.
Formula used:
The modulus of rigidity is given by:
$\eta = \dfrac{F}{A} . \dfrac{\Delta l}{l} $.

Complete answer:
The important point to solve this question is the geometry of the problem. We have to know which faces of our cuboidal brass plate suffer the tangential stresses. Here, we have a horizontal version of the plate in the diagram i.e., to consider the actual situation, one should rotate this picture by a right angle so that the plate stands vertically. Anyways, the shear acts in two opposite directions as shown which will be front and the back end of the plate if it were vertical.

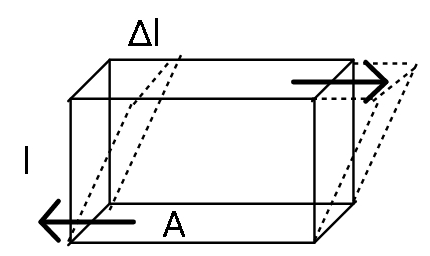
Modulus of rigidity for share modulus is the ratio of tangential stress acting on the body to shear strain that the body undergoes by the stress. The formula for modulus of rigidity will give us:
$F = \dfrac{\eta A \Delta l}{l}$.
Now, for brass, $\eta_{brass} = 3.5 \times 10^{10} N m^{-2}$. We are given, $\Delta l = 0.32 mm = 0.32 \times 10^{-3} m $, l = 1cm =0.01 m and A = 1.6 $m^2$.
Substituting these values in the formula, we write:
$F = \dfrac{3.5 \times 10^{10} \times 1.6 \times 0.32 \times 10^{-3} }{0.01} = 1.792 \times 10^9$N.
Therefore, this is the amount of parallel force that was applied to create a lateral displacement of 0.32 mm.

Note:
It might be a little confusing to find out the faces that undergo the parallel force action. In this case one can plainly keep all the given values in the simple formula for modulus of rigidity and obtain the answer but one does not get this lucky all the time so when should pay some attention and observe the geometry of the problem carefully.