Question

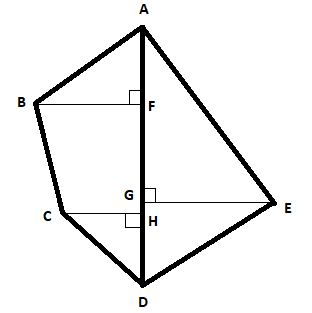
The following diagram shows a pentagonal field ABCDE in which the lengths of AF, FG, GH and HD are 50m, 40m, 15m and 25m respectively; and the lengths of perpendiculars BF, CH and EG are 50m, 25m, and 60m respectively. Determine the area of the field.

A) 7900sq.m
B) 7425 sq.m
C) 7750 sq.m
D) 7525 sq.m

Answer 1

Hint:
 We can divide the given field into a bigger triangle, a trapezium and 2 smaller triangles. Then we can find the area of each part separately. Then we can take the sum of all the areas to get the required area of the field.

Complete step by step solution:
We are given that the lengths of AF, FG, GH and HD are 50m, 40m, 15m and 25m respectively. So, we can write,
 $AF = 50m$, $FG = 40m$ , $GH = 15m$ and $HD = 25m$
It is also given that the lengths of perpendiculars BF, CH and EG are 50m, 25m, and 60m respectively. So, we can write,
 $BF = 50m$ , $CH = 25m$ and $EG = 60m$
From the figure, the area of the field is divided into a bigger triangle ADE, a trapezium BCHF and 2 smaller triangles ABF and CDH.
Now we can find the area of the triangle ADE.
We know that the area of a triangle is given by $A = \dfrac{1}{2}b \times h$ .
From the figure, AD is the base of the triangle ADE and EG is its height. So, we can write,
 $ \Rightarrow Area\left( {ADE} \right) = \dfrac{1}{2} \times AD \times EG$
From the figure, we can write AD as the sum of the known lengths.
 $ \Rightarrow Area\left( {ADE} \right) = \dfrac{1}{2} \times \left( {AF + FG + GH + HD} \right) \times EG$
On substituting the values, we get,
 $ \Rightarrow Area\left( {ADE} \right) = \dfrac{1}{2} \times \left( {50 + 40 + 15 + 25} \right) \times 60$
On simplification, we get,
 $ \Rightarrow Area\left( {ADE} \right) = 130 \times 30$
On simplification we get,
 $ \Rightarrow Area\left( {ADE} \right) = 3900{m^2}$
Now we can find the area of the triangle ABF.
From the figure, AF is its base and BF is the height.
 $ \Rightarrow Area\left( {ABF} \right) = \dfrac{1}{2} \times AF \times BF$
On substituting the values, we get,
 $ \Rightarrow Area\left( {ABF} \right) = \dfrac{1}{2} \times 50 \times 50$
On simplification, we get,
 $ \Rightarrow Area\left( {ABF} \right) = 50 \times 25$
On multiplication we get,
 $ \Rightarrow Area\left( {ABF} \right) = 1250{m^2}$
Now we can find the area of the trapezium BCHF.
We know that area of a trapezium is given by,
 $Area = \dfrac{1}{2} \times \left( {a + b} \right) \times h$
From the figure, FH is the height of the trapezium and BF and CH are the parallel sides. So, we can write the area of the trapezium as,
 $ \Rightarrow Area\left( {BCHF} \right) = \dfrac{1}{2} \times \left( {BF + CH} \right) \times FH$
From the figure, we can write AD as the sum of the known lengths.
 $ \Rightarrow Area\left( {BCHF} \right) = \dfrac{1}{2} \times \left( {BF + CH} \right) \times \left( {FG + GH} \right)$
On substituting the values, we get,
   $ \Rightarrow Area\left( {BCHF} \right) = \dfrac{1}{2} \times \left( {50 + 25} \right) \times \left( {40 + 15} \right)$
On simplification, we get,
 $ \Rightarrow Area\left( {BCHF} \right) = \dfrac{1}{2} \times 75 \times 55$
On further simplification we get,
 $ \Rightarrow Area\left( {BCHF} \right) = 2062.5{m^2}$
Now we can find the area of the triangle CDH.
From the figure, HD is its base and CH is the height.
 $ \Rightarrow Area\left( {CDH} \right) = \dfrac{1}{2} \times CH \times HD$
On substituting the values, we get,
 $ \Rightarrow Area\left( {CDH} \right) = \dfrac{1}{2} \times 25 \times 25$
On simplification, we get,
 $ \Rightarrow Area\left( {CDH} \right) = 312.5{m^2}$
Now we can take the sum of these areas to find the total area.
 $ \Rightarrow A = Area\left( {ABF} \right) + Area\left( {ADE} \right) + Area\left( {BCHF} \right) + Area\left( {CDH} \right)$
On substituting the values, we get,
 $ \Rightarrow A = 3900 + 1250 + 2062.5 + 312.5$
On simplification we get,
 $ \Rightarrow A = 7525{m^2}$
Therefore, the area of the field is $7525{m^2}$.

So, the correct answer is option D.

Note:
While dividing the field into different areas, we must make sure that an area is only considered once and no area is excluded. For that we must make sure that the smaller areas are edge to edge such that there is no gap between them or they overlap. We must take care while writing the longer length as the sum of the smaller length. Even though addition is commutative, we can write them in the same order to reduce the chances of errors.