Question

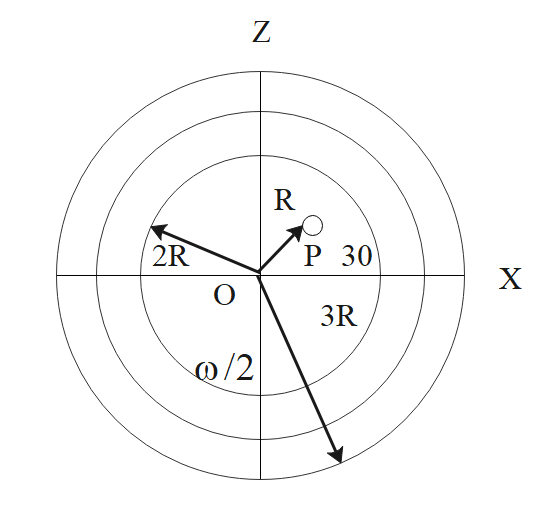
The figure shows in system consisting of (i) a ring of outer radius 3r rolling clockwise without slipping on a horizontal surface with angular speed $\omega $ and (ii) an inner disc of radius 2r rotating anti-clockwise with angular speed $\dfrac{\omega }{2}$. The ring and disc are separated by frictionless ball bearings. The system is in the x-z plane. The point p on the inner disc is at a distance r from the origin, where op makes an angle of ${{30}^{0}}$ with the horizontal. Then with respect to the horizontal surface,
A) the point o has a linear velocity $3R\omega \hat{i}$
B) the point p has linear velocity $\dfrac{11}{4}R\omega \hat{i}+\dfrac{\sqrt{3}}{4}R\omega \hat{k}$
C) the point p has linear velocity $\dfrac{11}{4}R\omega \hat{i}-\dfrac{\sqrt{3}}{4}R\omega \hat{k}$
D) none.

Answer 1

Hint: Let us first find the linear velocity of the point o that is at a distance r from the origin. Next, we need to find the velocity of p with respect to the centre of the object displayed. Next, the linear velocity of point p can be calculated by subtracting the relative velocity with the linear velocity at centre o.

Complete answer:
Let us first find the linear velocity of the figure at point o or the centre of the system,
Conserving the momentum in the x axis positive direction,
As the mass is same,
$\begin{align}
  & {{v}_{o}}-3R\omega \hat{i}=0 \\
 & \Rightarrow {{v}_{0}}=3R\omega \hat{i} \\
\end{align}$
Now, let us find the velocity of the point p with respect to centre o,
$\begin{align}
  & {{v}_{p,o}}=\dfrac{-R\omega }{4}\hat{i}+\dfrac{\sqrt{3}R\omega }{4}\hat{k} \\
 & \\
\end{align}$
Now, the velocity of p can be calculated as,
$\begin{align}
  & {{v}_{p}}={{v}_{p,o}}+{{v}_{o}} \\
 & \Rightarrow {{v}_{p}}=\dfrac{11R\omega }{4}\hat{i}+\dfrac{\sqrt{3}R\omega }{4}\hat{k} \\
\end{align}$

Therefore, the correct options are option a and option b.

Additional information:
Rigid body is an object of finite extent in which all the distances between the component particles are constant. If we take any rigid body in our real life, there is no truly rigid body because external forces can deform any solid material. For our calculations, a rigid body is a solid which requires large forces to deform it appreciably. Change in the position of rigid body can be described in 2 motions one is translational motion and the other is circular motion. Purely translational motion occurs when every particle of the body has the same velocity as every other particle. The path traced out by any particle is exactly parallel to the part traced out by every other particle in the body. Purely rotational motion occurs if every particle in the body moves in a circle about a single line. This line can be called the axis of rotation.

Note:
During some cases, we can see a body undergoing both translational and rotational motion. This case can be seen when there's certain frictional force acting at the surface of the rigid body. In that case we need to consider both translational and rotational motion at the same time.