Question

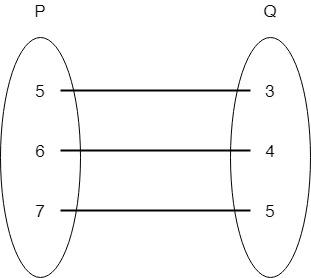
The figure shows a relationship between the sets P and Q. Write this relation in (i) in Set builder form (ii) Roster form

Answer 1

Hint: According to the given question, firstly observe the figure and then solve for the given parts. In set builder form we have to calculate the difference between the elements of the set P and Q, then write in the equation form. In roster form we just have the set builder form in number sets to get a roster form.

Complete step-by-step answer:
Here, we will firstly solve for (i) In set builder form
As it is clearly visible in the figure that \[5 - 3 = 2\] , \[6 - 4 = 2\] , \[7 - 5 = 2\]
Therefore, the difference of the elements of P and Q is the same that is 2.
So, let us suppose that the elements of set P can be denoted by x which means \[x \in P\] .
Similarly, let’s suppose that the elements of set Q can be denoted by y which means \[y \in Q\] .
Hence, We can conclude from the above that \[x - y = 2\] --equation 1.
Therefore, we write relation (R) in the set builder form.
R = \[\left\{ {\left( {x,y} \right):x - y = 2{\rm{ }}\,for\,{\rm{ }}\,x \in P{\rm{ }}and{\rm{ }}y \in Q} \right\}\] which is representation of set builder form.
Now, we will solve for (ii) In Roster form
As, it is clearly observed from the figure that relation R = \[\{ \left( {x,y} \right)\,where\,{\rm{ }}x \in P{\rm{ }}\,and\,{\rm{ }}y \in Q\} \]
So, we write above set builder form in the form of roster form.
Hence, R = \[\{ (5,3),(6,4),(7,5)\} \] which is a representation of roster form.

Note: To solve these types of questions, we must remember the representation of set builder form and the roster form. Here, we can also calculate for the domain which is the set of first elements of relation that is x values in a set and range which is the set of second elements of relation that are y values in a set. As in the above question domain is \[\left\{ {5,6,7} \right\}\] and range is \[\left\{ {3,4,5} \right\}\] .