Question

The figure shows a circuit

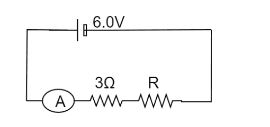
When the circuit is switched on the ammeter reads $0.5A$
(a) Calculate the value of an unknown resistor $R$.
(b) Calculate the charge passing through the $3 \Omega$ resistor in $120\,s$.
(c) Calculate the power dissipated in the $3 \Omega $ resistor.

Answer 1

Hint: for solving part (a) we will use ohm’s law. and for resistors in series total resistance in the circuit is the sum of the resistance produced by all the resistors . for part (b) using the current and charge relation we will find the charge. for part (c) use the formula for power dissipation.

Formula used:
$V = IR$ (ohm’s law)
Where $V$ is the voltage $I$ is current and $R$ is the resistance of the circuit.
$I = \dfrac{q}{t}$
Where $q$ is the charge and $t$ is the time
$P = {I^2}R$
Where $P$ is the power dissipated

Complete step by step answer:
(a) We have been given ammeter reading so current $I = 0.5A$ and $V = 6V$. According to ohm's law, the current in a conductor between two points is proportional to the voltage across these two points.
$V = IR'$..........( here $R'$ is the total resistance)
$ \Rightarrow 6 = 0.5 + R$
$ \Rightarrow R = 12\Omega $
In the given circuit the resistor let ${R_1} = 3\Omega $ and unknown resistance be $R$ . as they are in series
So, $R' = {R_1} + R$
$ \Rightarrow 12\Omega = 3\Omega + R$
$ \therefore R = 9\Omega $

(b) We have been given time $t = 120\,s$ so current will be given as,
$I = \dfrac{q}{t}$
$ \Rightarrow 0.5\,A = \dfrac{q}{{120\,s}}$
$ \therefore q = 6\,C$

(c) For the resistance of $3\Omega $ power dissipated will be
$P = {I^2}R$
$ \Rightarrow P = {\left( {0.5} \right)^2}(3)$
$ \therefore P = 0.75\,watt$

Note: if the resistors are in parallel total resistance is found out as $\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}}$. We can see in part B that the charge flowing through both the resistors is the same because in series combination current flowing through the different resistors is the same. if there was a parallel combination of resistors we have to find the charge flowing through different resistors separately.