Question

The exterior angle of a triangle is equal to sum of two
(a) Exterior angles
(b) Interior angles
(c) Interior opposite angles
(d) Alternate angles

Answer 1

Hint: We will take the help of the theorems of triangles to solve the question. First one is the sum of interior angles of any triangle is ${{180}^{\text{o}}}$. Second one is the angle on one line is ${{180}^{\text{o}}}$. The second theorem will be used by extending any line of a triangle so that we have one line with angles on it. For example we have a triangle ABC and we extend line AC then we will get two angles on that line. And those two angles will be ${{180}^{\text{o}}}$.

Complete step-by-step answer:
Before solving the question we will first understand the concept of exterior and interior angles. An exterior angle is an angle which is formed outside any triangle. On the other hand the interior angle is an angle which is formed inside any triangle. We will also come to know about the interior opposite angles. These angles are the angles which are formed on the alternate sides of the parallel lines. All these angles are drawn in the figure below.

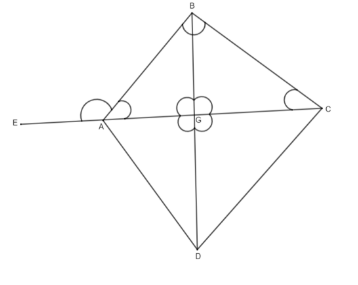
In this figure the exterior angle is $\angle BAE$, interior angle is $\angle ABG,\angle BGA,\angle GAB$ and the alternate angles are $\angle BGA,\angle CGD$ also $\angle BGC,\angle AGD$.
We need to find out that the exterior angle of a triangle is equal to the sum of two ___ angles. According to our figure we actually need to find out that the angle $\angle BAE$ is equal to what sum of angles. For this we will apply the theorems of triangles. First one is the sum of interior angles of any triangle is ${{180}^{\text{o}}}$. Here, we are going to consider the triangle $\Delta ABG$.
So, according to the figure the theorem will apply as $\angle BAG+\angle AGB+\angle GBA={{180}^{\text{o}}}$....(i). Now we will apply another theorem which is stated as the angle on one line is ${{180}^{\text{o}}}$. For example, we here have $\angle BAE+\angle BAG={{180}^{\text{o}}}$...(ii) and EAGC is one line. Since, the right side of the equation (i) and (ii) are equal so we have that the left side of the equations are also equal. So, we get that $\angle BAG+\angle AGB+\angle GBA=\angle BAE+\angle BAG$.
After cancelling the common terms from the equation which is $\angle BAG$ therefore, we now have $\angle AGB+\angle GBA=\angle BAE$. As the $\angle BAE$ is the exterior angle of the triangle $\Delta ABG$ and $\angle AGB,\angle GBA$ are the interior angles of the triangle $\Delta ABG$ so, we have found out that exterior angle of a triangle is equal to sum of two Interior angles.
Hence, the correct option is (c).

Note: We can also draw the figure by extending the line GC to the right and considering an exterior angle there. After this we can solve the question as usual. Similarly, if we can choose either side, then also we get the same result like we have got in the solution.One may argue option b is also correct but do remember that the angle corresponding to the exterior angle is also an interior angle however the sum do not include that angle hence option c is most appropriate answer.