Question

The equivalent capacitance between A and B in the circuit given below is:

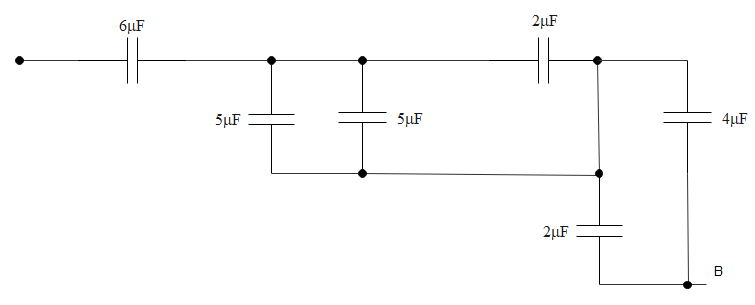
A. $\text{4}\text{.9 }\!\!\mu\!\!\text{ F}$
B. $\text{3}\text{.6 }\!\!\mu\!\!\text{ F}$
C. $\text{5}\text{.4 }\!\!\mu\!\!\text{ F}$
D. $\text{2}\text{.4 }\!\!\mu\!\!\text{ F}$

Answer 1

Hint: For solving this question, we need to make sure that the simplified diagram of the circuit is correct. On the basis of the simplified circuit, we can figure out the parallel connections and the series connections. This will ultimately lead to the development of the equivalent capacitance of the circuit.

Complete step by step answer:
 Before we move on with the solution of the question, we need to remember the following formulas, here are they:
Equivalent capacitance of the series circuit is denoted by ${{\text{C}}_{\text{series}}}$.
We should know that, ${{\text{C}}_{\text{series}}}\text{ = }\dfrac{\text{1}}{\dfrac{\text{1}}{{{\text{C}}_{\text{1}}}}\text{ + }\dfrac{\text{1}}{{{\text{C}}_{\text{2}}}}\text{ + }..............\text{ + }\dfrac{\text{1}}{{{\text{C}}_{\text{n}}}}}$${{\text{C}}_{\text{series}}}\text{ = }\dfrac{\text{1}}{\dfrac{\text{1}}{{{\text{C}}_{\text{1}}}}\text{ + }\dfrac{\text{1}}{{{\text{C}}_{\text{2}}}}\text{ + }..............\text{ + }\dfrac{\text{1}}{{{\text{C}}_{\text{n}}}}}$
Equivalent capacitance of the parallel circuit is denoted by ${{\text{C}}_{\text{parallel}}}$.
We should know that, ${{\text{C}}_{\text{parallel}}}\text{ = }{{\text{C}}_{\text{1}}}\text{ + }{{\text{C}}_{\text{2}}}\text{ + }..........\text{ + }{{\text{C}}_{\text{n}}}$
Now let us draw the simplified structure of the circuit that is given. We can draw it like the one shown below for ease in calculation.

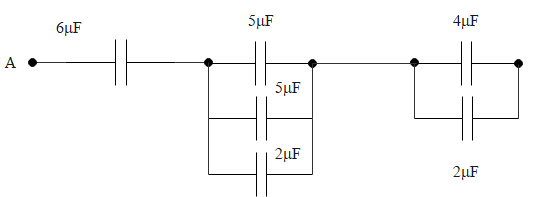
Therefore, we can determine the equivalent capacitance to be
${{\text{E}}_{\text{q}}}\text{ = 5 + 5 + 2 = 12 }\!\!\mu\!\!\text{ F}$
This is the equivalent capacitance of the capacitor bank in the middle of the circuit as given in the above diagram.

${{\text{E}}_{\text{q}}}\text{ = 4 + 2 = 8 }\!\!\mu\!\!\text{ F}$
This is the equivalent capacitance of the capacitor bank in the right end of the circuit as drawn above.

$\therefore$ Parallel connection of all the series equivalent capacitors rounds up to a total of
${{\text{E}}_{\text{q}}}\text{ = 2}\text{.4 }\!\!\mu\!\!\text{ F}$
Note: We should know the definition of the quantity that is mentioned in the question. By capacitance we mean the electric charge in a system, which is expressed in accordance to the electric potential value. The symbol of expression of capacitance is C. The unit of capacitance is Farad. Farad is the ratio between charge and voltage. The unit of charge is coulomb and that of the voltage is volts. So, Farad is coulomb divided by volts.