Question

The equation of the hyperbola whose foci are (6,5), (-4,5) and eccentricity $\dfrac{5}{4}$ is?
A. $\dfrac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{9} = 1$
B. $\dfrac{{{x^2}}}{{16}} - \dfrac{{{y^2}}}{9} = 1$
C. $\dfrac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{9} = 1$
D. $\dfrac{{{{\left( {x - 1} \right)}^2}}}{4} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{9} = 1$

Answer 1

Hint: First, we will assume the centre of the hyperbola, then find the midpoint of foci. So, by comparing we will get the values of ${a^2}$ and ${b^2}$ with the help of eccentricity given and put all these values in the equation of hyperbola to get the answer.

Complete step-by-step answer:

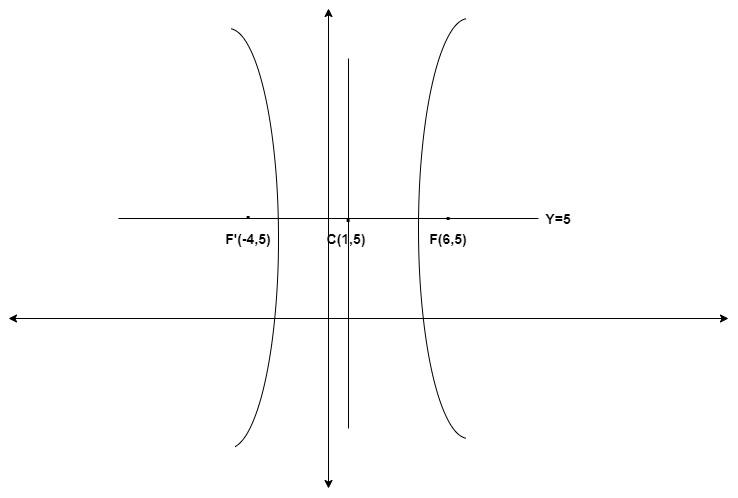
Let the centre of hyperbola be $\left( {\alpha ,\beta } \right)$
As we know that the coordinates of foci are (6,5), (-4,5). So, we can say that
y = 5 line has the focus on it, and it also has the major axis.
So, with the help of equation of hyperbola i.e. \[\dfrac{{{{\left( {x - h} \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - k} \right)}^2}}}{{{b^2}}} = 1\], where $\left( {h,k} \right)$ are the centre of hyperbola.
$\therefore \dfrac{{{{\left( {x - \alpha } \right)}^2}}}{{{a^2}}} - \dfrac{{{{\left( {y - \beta } \right)}^2}}}{{{b^2}}} = 1$ … (1)
We will use the property of hyperbola which says that the centre of hyperbola is equal to the midpoint of foci to find the value of $\alpha $ and $\beta $.
By using midpoint formula i.e. $\left( {{x_m},{y_m}} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$, we will find the midpoint of the foci i.e. (6,5), (-4,5) where ${x_1} = 6,{x_2} = - 4$ and ${y_1} = 5,{y_2} = 5$
Now, by using the midpoint formula
$\left( {{x_m},{y_m}} \right) = \left( {\dfrac{{6 - 4}}{2},\dfrac{{5 + 5}}{2}} \right) = \left( {1,5} \right)$
Now, by comparing this point with the centre of hyperbola i.e. $\left( {\alpha ,\beta } \right)$, we will get
$\alpha = 1$ and $\beta = 5$.
Given, $e = \dfrac{5}{4}$
We know that foci of hyperbola are given by $\left( { \pm ae,0} \right)$ for the centre as origin but our centre is not an origin. So, we will add the coordinates of centre in it to get the foci as $\left( {\alpha \pm ae,\beta } \right)$
Now, we will compare the x coordinates of these points (6,5) and $\left( {\alpha + ae,\beta } \right)$
$\therefore \alpha + ae = 6$, where $e = \dfrac{5}{4}$ and $\alpha = 1$
After, substituting we will get
$ \Rightarrow 1 + \dfrac{5}{4}a = 6$
Take L.C.M and by cross multiplying
$ \Rightarrow 4 + 5a = 6 \times 4$
Now, simplify the above equation
$
   \Rightarrow 5a = 24 - 4 \\
   \Rightarrow a = \dfrac{{20}}{5} = 4 \\
 $
Hence, by squaring both the sides ${a^2} = {4^2} = 16$
Since, we know that the eccentricity for hyperbola is $e = \dfrac{{\sqrt {{a^2} + {b^2}} }}{a}$
Now, by squaring both the sides
$ \Rightarrow {e^2} = \dfrac{{{a^2} + {b^2}}}{{{a^2}}}$
Further, by solving it
$
   \Rightarrow {e^2}{a^2} = {a^2} + {b^2} \\
   \Rightarrow {e^2}{a^2} - {a^2} = {b^2} \\
 $
We will take \[{a^2}\] common from L.H.S
$ \Rightarrow {a^2}\left( {{e^2} - 1} \right) = {b^2}$
Substitute the values of $a$ and $e$ in above equation
$
   \Rightarrow {b^2} = {4^2}\left( {{{\left( {\dfrac{5}{4}} \right)}^2} - 1} \right) \\
   \Rightarrow {b^2} = 16\left( {\dfrac{{25}}{{16}} - 1} \right) \\
 $
By taking L.C.M and after evaluating it
$ \Rightarrow {b^2} = 16\left( {\dfrac{{25 - 16}}{{16}}} \right)$
Cancel out the equal term from numerator and denominator
$ \Rightarrow {b^2} = 9$
We will put the values of ${a^2},{b^2}$ and $\alpha ,\beta $ in equation (1)
Therefore, equation of hyperbola is $\dfrac{{{{\left( {x - 1} \right)}^2}}}{{16}} - \dfrac{{{{\left( {y - 5} \right)}^2}}}{9} = 1$
Hence, the correct option is A.

Note: The hyperbola is two curves that are like infinite bows, where the conjugate axis is line perpendicular to the major axis or transverse axis i.e. line passing through foci. Conjugate axis cuts the hyperbola from the centre which proves the above mentioned property. Students must know all the terminology and formulas of the hyperbola, as usage of these formulas and properties are the only way to solve these kinds of questions.