
The equation \[\left| {z + i} \right| - \left| {z - i} \right| = k\] represents a hyperbola if
A.\[k \in \left( { - 2,2} \right)\]
B.\[k \in \left( { - 2,0} \right)\]
C.\[k \in \left\{ {0,2} \right\}\]
D.\[k \in \left\{ { - 2,2} \right\}\]
Answer
563.7k+ views
Hint: Here we need to find the range of the variable such that the equation will represent the equation of hyperbola. We will first assume the standard complex number and then we will substitute this value in the equation of the hyperbola. We will use the property of the hyperbola to find the range of the required variable.
Complete step-by-step answer:
The given equation is
\[\left| {z + i} \right| - \left| {z - i} \right| = k\] ……………. \[\left( 1 \right)\]
Here we need to find the range of \[k\] such that this equation will represent the equation of hyperbola.
Let the complex number \[z\] be \[x + iy\] .
Now, we will substitute this value in equation 1.
\[ \Rightarrow \left| {x + iy + i} \right| - \left| {x + iy - i} \right| = k\]
On simplifying the terms, we get
\[ \Rightarrow \left| {x + i\left( {y + 1} \right)} \right| - \left| {x + i\left( {y - 1} \right)} \right| = k\]
We know that \[\left| {a + ib} \right| = \sqrt {{a^2} + {b^2}} \]
Using this property of complex number, we get
\[ \Rightarrow \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = k\]
On further simplification, we get
\[ \Rightarrow \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = k - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
On squaring both sides, we get
\[ \Rightarrow {\left( {\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} } \right)^2} = {\left( {k - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} } \right)^2}\]
We know from the algebraic identities that \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
Using this identity here, we get
\[ \Rightarrow {x^2} + {\left( {y + 1} \right)^2} + 2 \times x \times \left( {y + 1} \right) = {k^2} + {\left( {\sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} } \right)^2} - 2 \times k \times \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
On further simplification, we get
\[ \Rightarrow {x^2} + {\left( {y + 1} \right)^2} = {k^2} + {x^2} + {\left( {y - 1} \right)^2} - 2 \times k \times \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
Now, again we will use the algebraic identities:-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
\[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]
\[ \Rightarrow {x^2} + {y^2} + 2y + 1 = {k^2} + {x^2} + {y^2} - 2y + 1 - 2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} \]
We will add and subtract the like terms on both sides
\[ \Rightarrow 2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} = {k^2} - 4y\]
On squaring both sides, we get
\[\begin{array}{l} \Rightarrow {\left( {2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} } \right)^2} = {\left( {{k^2} - 4y} \right)^2}\\ \Rightarrow 4{k^2}\left( {{x^2} + {y^2} - 2y + 1} \right) = {\left( {{k^2} - 4y} \right)^2}\end{array}\]
Now, we will use the the algebraic identity :-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
Using this identity, we get
\[ \Rightarrow 4{k^2}\left( {{x^2} + {y^2} - 2y + 1} \right) = {k^4} + 16{y^2} - 8y{k^2}\]
On multiplying the terms, we get
\[ \Rightarrow 4{k^2}{x^2} + 4{k^2}{y^2} - 8{k^2}y + 4{k^2} = {k^4} + 16{y^2} - 8y{k^2}\]
Now, we will add and subtract the like terms, we get
\[ \Rightarrow 4{k^2}{x^2} + \left( {4{k^2} - 16} \right){y^2} - {k^4} + 4{k^2} = 0\]…………… \[\left( 2 \right)\]
We know the general equation is given by
\[ \Rightarrow a{x^2} + b{y^2} + 2hxy + 2gx + 2fy + c = 0\] …………. \[\left( 3 \right)\]
We know that this general equation will represent the equation of hyperbola when \[{h^2} - ab > 0\]
Now, we will compare equation 2 and equation 3 i.e. we will compare the obtained equation with the general equation.
\[\begin{array}{l}a = 4{k^2}\\b = 4{k^2} - 16\\h = 0\\g = 0\\c = - {k^4} + 4{k^2}\end{array}\]
The obtained equation will represent the equation of hyperbola when \[{h^2} - ab > 0\]
Substituting \[h = 0,a = 4{k^2}\] and \[b = 4{k^2} - 16\] in the above equation, we get
\[{0^2} - \left( {4{k^2}} \right)\left( {4{k^2} - 16} \right) > 0\]
On further simplification, we get
\[ \Rightarrow - 4{k^2}\left( {4{k^2} - 16} \right) > 0\]
Multiplying \[ - 1\] to both sides of inequality
\[ \Rightarrow 4{k^2}\left( {4{k^2} - 16} \right) < 0\]
We can write this inequality as
\[ \Rightarrow 16{k^2}\left( {k - 2} \right)\left( {k + 2} \right) < 0\]
Now, we will number lines to solve this inequality.
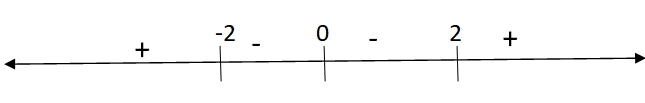
We can see from the number line that \[k \in \left( { - 2,2} \right)\] is satisfying the inequality.
Hence, the \[k \in \left( { - 2,2} \right)\] is the required answer.
Therefore, the correct option is option A.
Note: To solve this question, we need to know the basic properties of the hyperbola and how a general equation is used for different equations. Here we have also solved the inequality to get the required value. When we divide or multiply a negative number on both sides of the inequality, the sign of inequality gets changed but when we add or subtract the number on both sides of the inequality, the sign of inequality remains unchanged.
Complete step-by-step answer:
The given equation is
\[\left| {z + i} \right| - \left| {z - i} \right| = k\] ……………. \[\left( 1 \right)\]
Here we need to find the range of \[k\] such that this equation will represent the equation of hyperbola.
Let the complex number \[z\] be \[x + iy\] .
Now, we will substitute this value in equation 1.
\[ \Rightarrow \left| {x + iy + i} \right| - \left| {x + iy - i} \right| = k\]
On simplifying the terms, we get
\[ \Rightarrow \left| {x + i\left( {y + 1} \right)} \right| - \left| {x + i\left( {y - 1} \right)} \right| = k\]
We know that \[\left| {a + ib} \right| = \sqrt {{a^2} + {b^2}} \]
Using this property of complex number, we get
\[ \Rightarrow \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} = k\]
On further simplification, we get
\[ \Rightarrow \sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} = k - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
On squaring both sides, we get
\[ \Rightarrow {\left( {\sqrt {{x^2} + {{\left( {y + 1} \right)}^2}} } \right)^2} = {\left( {k - \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} } \right)^2}\]
We know from the algebraic identities that \[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
Using this identity here, we get
\[ \Rightarrow {x^2} + {\left( {y + 1} \right)^2} + 2 \times x \times \left( {y + 1} \right) = {k^2} + {\left( {\sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} } \right)^2} - 2 \times k \times \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
On further simplification, we get
\[ \Rightarrow {x^2} + {\left( {y + 1} \right)^2} = {k^2} + {x^2} + {\left( {y - 1} \right)^2} - 2 \times k \times \sqrt {{x^2} + {{\left( {y - 1} \right)}^2}} \]
Now, again we will use the algebraic identities:-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
\[{\left( {a + b} \right)^2} = {a^2} + {b^2} + 2ab\]
\[ \Rightarrow {x^2} + {y^2} + 2y + 1 = {k^2} + {x^2} + {y^2} - 2y + 1 - 2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} \]
We will add and subtract the like terms on both sides
\[ \Rightarrow 2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} = {k^2} - 4y\]
On squaring both sides, we get
\[\begin{array}{l} \Rightarrow {\left( {2 \times k \times \sqrt {{x^2} + {y^2} - 2y + 1} } \right)^2} = {\left( {{k^2} - 4y} \right)^2}\\ \Rightarrow 4{k^2}\left( {{x^2} + {y^2} - 2y + 1} \right) = {\left( {{k^2} - 4y} \right)^2}\end{array}\]
Now, we will use the the algebraic identity :-
\[{\left( {a - b} \right)^2} = {a^2} + {b^2} - 2ab\]
Using this identity, we get
\[ \Rightarrow 4{k^2}\left( {{x^2} + {y^2} - 2y + 1} \right) = {k^4} + 16{y^2} - 8y{k^2}\]
On multiplying the terms, we get
\[ \Rightarrow 4{k^2}{x^2} + 4{k^2}{y^2} - 8{k^2}y + 4{k^2} = {k^4} + 16{y^2} - 8y{k^2}\]
Now, we will add and subtract the like terms, we get
\[ \Rightarrow 4{k^2}{x^2} + \left( {4{k^2} - 16} \right){y^2} - {k^4} + 4{k^2} = 0\]…………… \[\left( 2 \right)\]
We know the general equation is given by
\[ \Rightarrow a{x^2} + b{y^2} + 2hxy + 2gx + 2fy + c = 0\] …………. \[\left( 3 \right)\]
We know that this general equation will represent the equation of hyperbola when \[{h^2} - ab > 0\]
Now, we will compare equation 2 and equation 3 i.e. we will compare the obtained equation with the general equation.
\[\begin{array}{l}a = 4{k^2}\\b = 4{k^2} - 16\\h = 0\\g = 0\\c = - {k^4} + 4{k^2}\end{array}\]
The obtained equation will represent the equation of hyperbola when \[{h^2} - ab > 0\]
Substituting \[h = 0,a = 4{k^2}\] and \[b = 4{k^2} - 16\] in the above equation, we get
\[{0^2} - \left( {4{k^2}} \right)\left( {4{k^2} - 16} \right) > 0\]
On further simplification, we get
\[ \Rightarrow - 4{k^2}\left( {4{k^2} - 16} \right) > 0\]
Multiplying \[ - 1\] to both sides of inequality
\[ \Rightarrow 4{k^2}\left( {4{k^2} - 16} \right) < 0\]
We can write this inequality as
\[ \Rightarrow 16{k^2}\left( {k - 2} \right)\left( {k + 2} \right) < 0\]
Now, we will number lines to solve this inequality.
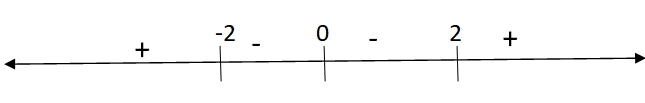
We can see from the number line that \[k \in \left( { - 2,2} \right)\] is satisfying the inequality.
Hence, the \[k \in \left( { - 2,2} \right)\] is the required answer.
Therefore, the correct option is option A.
Note: To solve this question, we need to know the basic properties of the hyperbola and how a general equation is used for different equations. Here we have also solved the inequality to get the required value. When we divide or multiply a negative number on both sides of the inequality, the sign of inequality gets changed but when we add or subtract the number on both sides of the inequality, the sign of inequality remains unchanged.
Recently Updated Pages
Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Master Class 11 Physics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Discuss the various forms of bacteria class 11 biology CBSE

Draw a diagram of a plant cell and label at least eight class 11 biology CBSE

State the laws of reflection of light

Explain zero factorial class 11 maths CBSE

10 examples of friction in our daily life




