Question

The ellipse ${x^2} + 4{y^2} = 4$ is inscribed in a rectangle aligned with the coordinate axes. Which is inscribed in another ellipse that passes through the point (4,0). Then the equation of the ellipse is
$
  A.\,{x^2} + 16{y^2} = 16 \\
  B.\,{x^2} + 12{y^2} = 16 \\
  C.\,4{x^2} + 48{y^2} = 48 \\
  D.\,4{x^2} + 64{y^2} = 48 \\
$

Answer 1

Hint: In order to solve this problem we need to draw a rough figure and analyze from the figure of various values. Here from the given equation we will find major and minor axes of smaller ellipse and from which we can find a point through which required ellipse passes that will give us the equation of the new ellipse.

Complete step by step solution:
The given equation of the ellipse is ${x^2} + 4{y^2} = 4$. It also can be written as,
$\dfrac{{{x^2}}}{4} + \dfrac{{{y^2}}}{1} = 1$. So, we can clearly see that the (2,0) and (0,1) are the coordinates of the longer and shorter axis of the ellipse.
So, we can draw the diagram as:

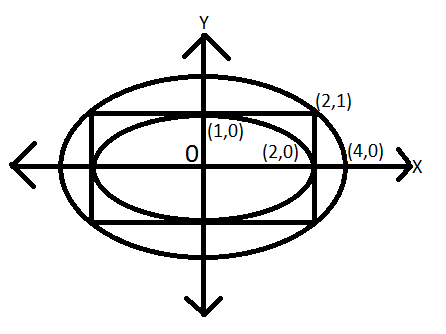
We only mentioned some of the points which will give you the information about other points and will help you to get the equation of the larger ellipse.
It is very clear that the length of the larger axis of the larger ellipse will be 4 and that of the other let us assume as b. Also the larger ellipse has a centre at (0,0). So, the equation of ellipse can be,
$\dfrac{{{x^2}}}{{{4^2}}} + \dfrac{{{y^2}}}{{{b^2}}} = 1$………..(1)
Now we need to find the value of b to get the equation.
As we know that the larger ellipse also passes through the point (2,1).
So we do,
$
  \dfrac{{{2^2}}}{{{4^2}}} + \dfrac{{{1^2}}}{{{b^2}}} = 1 \\
  \dfrac{1}{{{b^2}}} = 1 - \dfrac{1}{4} = \dfrac{3}{4} \\
  {b^2} = \dfrac{4}{3} \\
$
So, the value of ${b^2}$ is $\dfrac{4}{3}$.
On putting this value in equation (1) we get the new equation as,
$
  \dfrac{{{x^2}}}{{16}} + \dfrac{{{y^2}}}{{\dfrac{4}{3}}} = 1 \\
  \dfrac{{{x^2}}}{{16}} + \dfrac{{12{y^2}}}{{16}} = 1 \\
$
Multiplying the terms of y with 4 to get the same denominator above the equation is obtained.
So, the required equation is,
${x^2} + 12{y^2} = 16$
So, the correct option is B.

Note: When you get to solve such problems you need to obtain the various equations to get the value of variables using the information given in question and analysing the figure. In such problems figures play a pivotal role in getting the right answer. Since it provides the exact situation if it is drawn correctly. So, apart from assuming the figure in mind, drawing it will be more helpful to get the right answer.