Question

The effective resistance of a circuit containing resistances in a parallel connection is:
  ${\text{A}}{\text{.}}$ equal to the sum of individual resistances
  ${\text{B}}{\text{.}}$ smaller than any of the individual resistances
  ${\text{C}}{\text{.}} $ greater than any of the individual resistances
  ${\text{D}}{\text{.}}$ sometimes greater and sometimes smaller than the individual resistances

Answer 1

Hint: To determine the effective resistance we consider a circuit with resistors in parallel connection having each individual resistance of some variable and then we find the effective resistance of the circuit using the definition of a parallel connection.
Formula Used:
Effective resistance - $\dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{1}{{{{\text{R}}_1}}} + \dfrac{1}{{{{\text{R}}_2}}} + \dfrac{1}{{{{\text{R}}_3}}}$

Complete Step-by-Step solution:
A parallel connection is when all the components are connected across each other’s leads. Every component is connected in an individual path, all the individual paths have no more than two sets of electrically common points no matter how many ever components the circuit has.
The current that flows in each path of a parallel connected circuit is not necessarily the same but the sum of currents flowing across each path is equal to the total current that flows from the source.
Let us consider a circuit with three different resistances connected in parallel as shown in the figure:

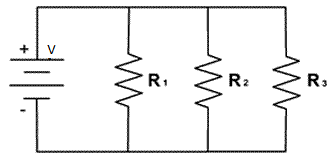
The total resistance of a parallel connection is given by the formula –
$\dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{1}{{{{\text{R}}_1}}} + \dfrac{1}{{{{\text{R}}_2}}} + \dfrac{1}{{{{\text{R}}_3}}}$, where ${{\text{R}}_{\text{t}}}$is the effective resistance of the circuit and ${{\text{R}}_1},{{\text{R}}_2}{\text{ and }}{{\text{R}}_3}$ are the individual resistances in the circuit.

Now let us take some random values of ${{\text{R}}_1},{{\text{R}}_2}{\text{ and }}{{\text{R}}_3}$and find the effective resistance to compare it with the individual resistances and find the answer.
Let, ${{\text{R}}_1}$= 2Ω, ${{\text{R}}_2}$= 3Ω and ${{\text{R}}_3}$= 4Ω
Now the effective resistance ${{\text{R}}_{\text{t}}}$is:
$
   \Rightarrow \dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{1}{{{{\text{R}}_1}}} + \dfrac{1}{{{{\text{R}}_2}}} + \dfrac{1}{{{{\text{R}}_3}}} \\
   \Rightarrow \dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} \\
   \Rightarrow \dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{{6 + 4 + 3}}{{12}} \\
   \Rightarrow \dfrac{1}{{{{\text{R}}_{\text{t}}}}} = \dfrac{{13}}{{12}} \\
   \Rightarrow {{\text{R}}_{\text{t}}} = \dfrac{{12}}{{13}} \\
$
On comparing with individual resistances we get, ${{\text{R}}_{\text{t}}} < {{\text{R}}_1},{\text{ }}{{\text{R}}_{\text{t}}} < {{\text{R}}_2}{\text{ and }}{{\text{R}}_{\text{t}}} < {{\text{R}}_3}$. The effective resistance is always less than any of the individual resistances.
Hence Option B is the correct answer.

Note – In order to answer this type of question the key is to know the formula of effective resistance in a parallel connection.
In a parallel connection even if one of the paths broke and is dysfunctional, current keeps flowing in all the remaining paths keeping them functional. This is one of the main reasons circuits are connected in parallel in daily life usage because several components can be independent of each other.
Parallel circuits are used in so many daily life examples like wiring lights in a building/house, use a charger to a mobile or plug anything to a supply etc.