Question

The eccentricity of the ellipse, which meets the straight line $\dfrac{x}{7}+\dfrac{y}{7}=1$ on the axis of x and the straight line $\dfrac{x}{3}-\dfrac{y}{5}=1$ on the axis of y and whose axes lie along the axes of coordinates, is
  (a) $\dfrac{3\sqrt{2}}{7}$
  (b) $\dfrac{2\sqrt{6}}{7}$
  (c) $\dfrac{\sqrt{3}}{7}$
  (d) None of these.

Answer 1

Hint: Draw a rough diagram and try to find the lengths of the semi-major axis and the semi-minor axis of the ellipse. After you find them use the formula of eccentricity to get the answer.

Complete step-by-step solution -
Starting by drawing a rough diagram:

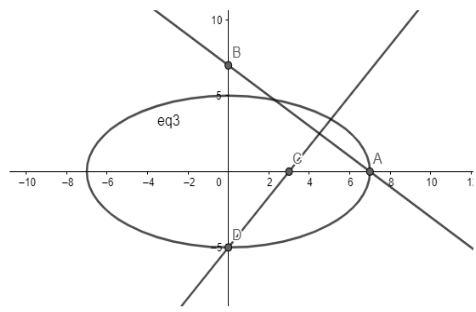
Now let us try to relate the diagram with the question.
From the figure, it is clear that the major axis of the ellipse is the x-axis, and the minor axis is the y-axis. Hence, the meeting point of the axes is O(0,0), which becomes the centre of the ellipse.
The equations of lines given in the question are the intercept form of the line. A general line can be represented in intercept form as $\dfrac{x}{a}+\dfrac{y}{b}=1$ , where a and b are the x-intercepts and the y-intercepts, respectively.
Therefore, the line $\dfrac{x}{7}+\dfrac{y}{7}=1$ meets x-axis at A(7,0), and as the ellipse meets this line on the x-axis, one of the vertex of the ellipse is A(7,0). Also, from here we can say that the length of the semi-major axis of the ellipse is 7.
Similarly, the other line in the question is also in its intercept form with y-intercept as -5, and the ellipse meets this line and the y-axis at D(0,-5), making the length of the semi-minor axis to be 5.
Now the eccentricity of an ellipse is given by the formula: $e=\sqrt{1-\dfrac{{{\left( \text{length of semi-minor axis} \right)}^{2}}}{{{\left( \text{length of semi-major axis} \right)}^{2}}}}$ . Using this formula, we get
 \[e=\sqrt{1-\dfrac{{{5}^{2}}}{{{7}^{2}}}}=\sqrt{1-\dfrac{25}{49}}=\sqrt{\dfrac{24}{49}}\]
We can conclude that the eccentricity of the ellipse asked in the question is $\sqrt{\dfrac{24}{49}}$ which is equal to $\dfrac{2\sqrt{6}}{7}$ . Hence, the answer is option (b).

Note: In such questions, the key is the diagram. If you get the diagram right, then you are most likely to reach an answer. Also, you must know the required formulas related to the figure and the different forms in which you can represent different geometrical shapes.