Question

The distance of the chord of length \[16 cm\] from the centre of the circle of diameter \[20 cm\] is:
A.\[3 cm\]
B.\[4 cm\]
C.\[5 cm\]
D.\[6 cm\]

Answer 1

Hint: We will find the perpendicular distance of the chord from the diameter by using the Pythagoras theorem in the triangle. After solving this we will get two values , negative values should be ignored as the distance can never be negative.

Formula used:
We will use the Pythagoras theorem that is \[{H^2} = {P^2} + {B^2}\].

Complete step-by-step answer:
Let's assume a circle with diameter $20\;{\text{cm}}$ with centre $O$. A chord $AB$ is drawn inside the circle as shown below:

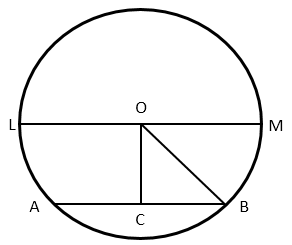
As given, that diameter is $20\;{\text{cm}}$, the radius of the circle $O$ will be half of diameter.
$ \Rightarrow {\text{Radius}}\;OM = \dfrac{{20}}{2}$
 $ = 10\;{\text{cm}}$
 As given, the chord $AB$ is $16{\kern 1pt} \;{\text{cm}}$, half of the chord will be $CB = 8\,cm$.
 Now, Consider the triangle $OCB$,
 Since radius $OM$ is equal to $OB$, then
$OB = 10\;{\text{cm}}$
  Now, we will use Pythagoras theorem to find the distance $OC$ that is the distance of the chord from the diameter.
$O{B^2} = O{C^2} + C{B^2}$ $\left( 1 \right)$
 Now substitute the values of $CB$ and $OB$ in the equation $\left( 1 \right)$.
 \[ \Rightarrow {\left( {10} \right)^2} = O{C^2} + {\left( 8 \right)^2}\]
 $100 = O{C^2} + 64$
 Simplify further to get the value of $OC$
$\Rightarrow$ $O{C^2} = 100 - 64$
$\Rightarrow$ $O{C^2} = 36$
Now, Take square roots on both sides of the above equation.
$\Rightarrow$ $OC = \pm 6$
 As the distance can never be negative. Therefore ignore $ - 6$ as the value of $OC$. So the length of $OC = 6\;{\text{cm}}$.
Therefore, the distance of chord from the diameter is $6\,cm$.
 So, option (D) is the correct answer.

Note: In these types of questions, first draw the situation given and then proceed. Also keep in mind that the line connected from centre to anywhere on the circumference will be equal to radius of that circle.
Also, always use Pythagoras theorem to find the unknown values in the triangles created.