Question

The dipper in a ripple tank vibrates at a frequency of 4.0Hz and the resulting wave pattern is photographed. The distance between the two crests shown is 20cm. What is the speed of the wave ?

A. $4{\text{ cm }}{{\text{s}}^{ - 1}}$
B. ${\text{5 cm }}{{\text{s}}^{ - 1}}$
C. ${\text{16 cm }}{{\text{s}}^{ - 1}}$
D. ${\text{20 cm }}{{\text{s}}^{ - 1}}$

Answer 1

Hint: For any kind of wave there will be maximum displacement position which is called crest and negative maximum position which is called trough. The distance between two successive crests or between two successive troughs is called wavelength of the wave. If we have frequency then we can find velocity too.

Formula used: $v = f\lambda $

Complete step by step answer:
There are two kinds of waves normally. One will be a transverse wave and the other will be a longitudinal wave. In case of transverse waves the direction of propagation of waves is perpendicular to the direction of vibration of the particles of the medium. Transverse wave has crests and troughs. In case of the longitudinal wave particles of the medium of propagation vibrates in the direction of propagation of the wave. This longitudinal wave has compressions and rarefactions. In case of longitudinal waves particles vibrate in to and fro motion. Transverse waves can propagate without medium too whereas longitudinal waves require medium to propagate. Example for transverse waves is light whereas example for the longitudinal wave is sound.
Velocity of sound depends upon density mainly. As density of the medium increases sound travelling velocity also increases.
When density is constant we have this formula to find out the velocity of a wave. The formula is
$v = f\lambda $
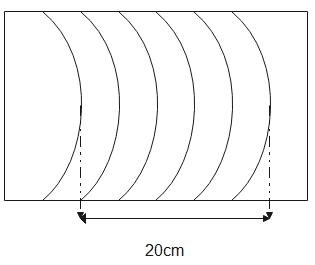
If we see the diagram distance between 5 crests is given as 20cm.
So
$\eqalign{
  & 5\lambda = 20cm \cr
  & \therefore \lambda = 4cm \cr} $
Frequency is given as 4 hertz.
So the velocity will be
$\eqalign{
  & v = f\lambda \cr
  & \Rightarrow v = 4 \times 4 \cr
  & \therefore v = 16{\text{ cm }}{{\text{s}}^{ - 1}} \cr} $

So, the correct answer is “Option C”.

Note: Whether it is a transverse wave or longitudinal wave, we can represent both in a sine function. We can represent them using sine waves. Distance between the zero displacement point to consecutive zero displacement point also gives us the wavelength of the wave. Magnitude of displacement will be minimum here.