Question

The dimensions of a Box are 1m, 80cm & 50cm. Find the area of its four walls.

Answer 1

Hint: We will be using the concept of mensuration to solve the problem. We will be using the area of the rectangle to find the area of four walls. We will also be using the fact that the area of parallel walls are the same in a cuboid.

Complete step-by-step solution -
Now, we have been given the dimensions of the box as 1m , 80cm and 50cm. So, now according to this the box is,

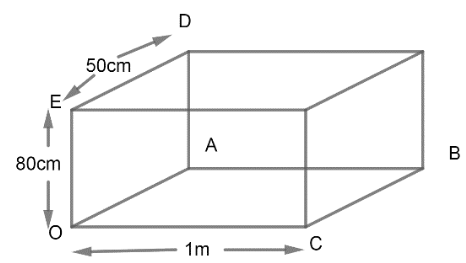
Now, we know that the area of a rectangle having length l and breadth b is lb sq units.
Now, in rectangle OABC we have,
$\begin{align}
  & Length=l=1m \\
 & Breadth=b=50cm=\dfrac{50}{100}m=\dfrac{1}{2}m \\
\end{align}$
Now, the area of walls OABC,
$\begin{align}
  & =l\times b \\
 & =1\times \dfrac{1}{2} \\
 & =\dfrac{1}{2}{{m}^{2}} \\
\end{align}$
We know that areas of parallel walls are the same in a cuboid. Therefore, the area of 2 walls are $\dfrac{1}{2}{{m}^{2}}$.
Now, in rectangle EDAO we have,
$\begin{align}
  & Length=l=\dfrac{80}{100}cm=\dfrac{8}{10}m=\dfrac{4}{5}m \\
 & Breadth=b=\dfrac{50}{100}m=\dfrac{1}{2}m \\
\end{align}$
Now, the area of walls EDAO,
$\begin{align}
  & =l\times b \\
 & =\dfrac{4}{5}\times \dfrac{1}{2} \\
 & =\dfrac{2}{5}{{m}^{2}} \\
\end{align}$
Now, the area of the wall parallel to this wall will also be the same, that is $\dfrac{2}{5}{{m}^{2}}$.
Therefore, area of two walls is $\dfrac{1}{2}{{m}^{2}}$ and other two walls is $\dfrac{2}{5}{{m}^{2}}$.

Note: To solve these types of questions it is important to draw a diagram which clearly shows the situation and then apply the formula of the area of the rectangle to find the answer. In cuboids the opposite faces are to be parallel so no need to find the area of all faces,here we only find any one face out of parallel faces.