Question

The difference of CSA of hollow cylinders whose h is 14 cm is $44c{m^2}$ and difference of volumes is $99c{m^3}$. Find the radii of the hollow cylinder.

Answer 1

Hint:
We can take the 2 radii as two variables. Then we can find their curved surface areas and equate their difference to the given value. Similarly, we can find the volume and equate their difference to the given value. Then we can obtain 2 equations in 2 variables. Then we can solve them to get the radii.

Complete step by step solution:
We can draw a diagram representing the 2 cylinders.

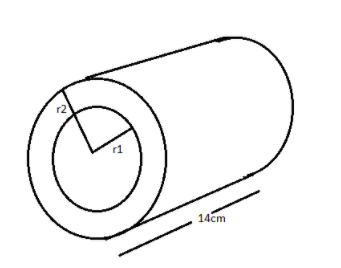
Let the radius of the smaller cylinder be ${r_1}$ and the radius of the smaller cylinder be ${r_2}$ .
It is given that the height of the cylinders is 14cm.
 $ \Rightarrow h = 14cm$
Now we can find the curved surface area of the smaller cylinder.
 $ \Rightarrow CS{A_1} = 2\pi rh$
On substituting the values, we get,
 $ \Rightarrow CS{A_1} = 2 \times \dfrac{{22}}{7} \times {r_1} \times 14$
On simplification, we get,
 $ \Rightarrow CS{A_1} = 88{r_1}$
Now we can find the curved surface area of the bigger cylinder.
 $ \Rightarrow CS{A_2} = 2\pi rh$
On substituting the values, we get,
 \[ \Rightarrow CS{A_2} = 2 \times \dfrac{{22}}{7} \times {r_2} \times 14\]
On simplification, we get,
 $ \Rightarrow CS{A_2} = 88{r_2}$
It is given that their difference is $44c{m^2}$ . So, we can write,
 $ \Rightarrow CS{A_2} - CS{A_1} = 44$
On substituting the values, we get,
 $ \Rightarrow 88{r_2} - 88{r_1} = 44$
On simplification, we get,
 $ \Rightarrow 88\left( {{r_2} - {r_1}} \right) = 44$
Dividing both sides with 88, we get,
 $ \Rightarrow {r_2} - {r_1} = \dfrac{{44}}{{88}}$
On simplification, we get,
 $ \Rightarrow {r_2} - {r_1} = \dfrac{1}{2}$
On rearranging, we get
 $ \Rightarrow {r_2} = \dfrac{1}{2} + {r_1}$ … (1)
On squaring both sides, we get,
 $ \Rightarrow {r_2}^2 = {\left( {\dfrac{1}{2} + {r_1}} \right)^2}$
On applying the identity, ${\left( {a + b} \right)^2} = {a^2} + 2ab + {b^2}$ , we get,
 $ \Rightarrow {r_2}^2 = {r_1}^2 + \dfrac{1}{4} + {r_1}$ … (2)
Now we can find the volume of the smaller cylinder.
 $ \Rightarrow {V_1} = \pi {r^2}h$
On substituting the values, we get,
 $ \Rightarrow {V_1} = \dfrac{{22}}{7} \times {r_1}^2 \times 14$
On simplification, we get,
 $ \Rightarrow {V_1} = 44{r_1}^2$
Now we can find the volume of the larger cylinder.
 $ \Rightarrow {V_2} = \pi {r^2}h$
On substituting the values, we get,
 $ \Rightarrow {V_2} = \dfrac{{22}}{7} \times {r_2}^2 \times 14$
 $ \Rightarrow {V_2} = 44{r_2}^2$
It is given that the difference in their volume is $99c{m^3}$ . So, we can write,
 $ \Rightarrow {V_2} - {V_1} = 99$
On substituting the values,
 $ \Rightarrow 44{r_2}^2 - 44{r_1}^2 = 99$
We can divide throughout with 44,
 $ \Rightarrow {r_2}^2 - {r_1}^2 = \dfrac{{99}}{{44}}$
On simplification, we get,
 $ \Rightarrow {r_2}^2 - {r_1}^2 = \dfrac{9}{4}$ … (3).
On substituting equation (2) in (3), we get,
 $ \Rightarrow {r_1}^2 + \dfrac{1}{4} + {r_1} - {r_1}^2 = \dfrac{9}{4}$
On simplification, we get,
 $ \Rightarrow {r_1} = \dfrac{9}{4} - \dfrac{1}{4}$
As the denominators are the same, we can subtract the numerators.
 $ \Rightarrow {r_1} = \dfrac{{9 - 1}}{4}$
So, we get,
 $ \Rightarrow {r_1} = \dfrac{8}{4}$
On simplification, we get,
 $ \Rightarrow {r_1} = 2$
On substituting this inequation (1), we get,
 $ \Rightarrow {r_2} = \dfrac{1}{2} + 2$
On simplification, we get,
 $ \Rightarrow {r_2} = 0.5 + 2$
Hence, we have,
 $ \Rightarrow {r_2} = 2.5$
Therefore, the radii of the cylinders are 2cm and 2.5cm.

Note:
We must find the curved surface area and volume of the cylinders separately and take their difference. While simplifying the volume, we must not take the difference of the squares as the square of the differences.

Alternate method of solving the equations is,
We have,
 $ \Rightarrow {r_2} = \dfrac{1}{2} + {r_1}$ … (a)
And,
 $ \Rightarrow {r_2}^2 - {r_1}^2 = \dfrac{9}{4}$
On applying the identity, \[{a^2} - {b^2} = (a + b)(a - b)\] , we get,
 $ \Rightarrow \left( {{r_2} - {r_1}} \right)\left( {{r_2} + {r_1}} \right) = \dfrac{9}{4}$
Now we can substitute equation (a)
 $ \Rightarrow \left( {\dfrac{1}{2} + {r_1} - {r_1}} \right)\left( {\dfrac{1}{2} + {r_1} + {r_1}} \right) = \dfrac{9}{4}$
On simplification, we get,
 $ \Rightarrow \left( {\dfrac{1}{2}} \right)\left( {\dfrac{1}{2} + 2{r_1}} \right) = \dfrac{9}{4}$
On expanding the bracket and multiplying, we get,
 $ \Rightarrow \dfrac{1}{4} + {r_1} = \dfrac{9}{4}$
On rearranging, we get,
 $ \Rightarrow {r_1} = \dfrac{9}{4} - \dfrac{1}{4}$
As the denominators are the same, we can subtract the numerators.
 $ \Rightarrow {r_1} = \dfrac{{9 - 1}}{4}$
So, we have,
 $ \Rightarrow {r_1} = \dfrac{8}{4}$
On simplification, we get,
 $ \Rightarrow {r_1} = 2$
On substituting this inequation (a), we get,
 $ \Rightarrow {r_2} = \dfrac{1}{2} + 2$
On simplification, we get,
 $ \Rightarrow {r_2} = 0.5 + 2$
So, we have,
 $ \Rightarrow {r_2} = 2.5$
Therefore, the radii of the cylinders are 2cm and 2.5cm.