Question

The difference between the radii of the largest and the smallest circles which have their centers on the circumference of the circles \[{x^2} + {y^2} + {\rm{2}}x + {\rm{4}}y - {\rm{4}} = {\rm{0}}\] and pass through the points $\left( {a,b} \right)$ lying outside the circle is
(A). 3
(B). 6
(C). 5
(D). None of these

Answer 1

Hint: Consider point \[\left( {{\rm{a}},{\rm{b}}} \right)\] as P and Q be the nearest point on the circumference of the circle to point P. Then the farthest will be just opposite to point Q, let’s say R so the distance between them will be the difference between radii of largest and smallest circle.

Complete step-by-step solution -
In the question we are asked to find out the difference between the radii of the largest and the smallest circles which have their centers on the circumference of the circle ${x^2} + {y^2} + {\rm{2}}x + {\rm{4}}y - {\rm{4}} = {\rm{0}}$ and also passes through the point \[\left( {{\rm{a}},{\rm{ b}}} \right)\] lying outside the given circle.
The equation of the given circle is ${x^2} + {y^2} + {\rm{2}}x + {\rm{4}}y - {\rm{4}} = {\rm{0}}$
We will first write it in form of ${\left( {x - {x_1}} \right)^2} + {\left( {y - {y_1}} \right)^2}{\rm{ = }}{{\rm{r}}^2}$ where center is \[\left( {{{\rm{x}}_{\rm{1}}},{\rm{ }}{{\rm{y}}_{\rm{1}}}} \right)\]and radius is r.
So we can rewrite the equation of circle as,
\[{x^2} + {\rm{2}}x + 1 + {y^2} + {\rm{4}}y + 4 - 1 - 4 - 4 = {\rm{0}}\]
Or, \[{\left( {x + 1} \right)^2} + {\left( {y + 2} \right)^2} = 9 = {3^2}\]
So the center of the circle is \[\left( { - {\rm{1}}, - {\rm{2}}} \right)\] and radius is 3.
So let’s say that the point \[\left( {{\rm{a}},{\rm{b}}} \right)\]as P. We will represent it as,
Here we assumed R be the farthest point from the given point P and Q be the nearest point from the point P. In the figure P is placed in \[{{\rm{1}}^{{\rm{st}}}}\] quadrant which is not necessary.

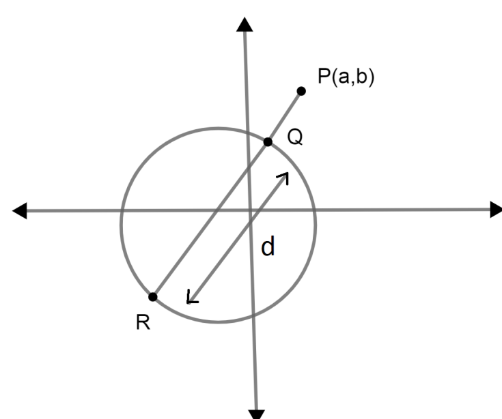
Here d is the distance between Q and R and also the diameter of the circle.
If Q is the nearest point from P then according to that R will be the farthest as R and Q will farthest only when they are extremities of the diameter of the circle.
So, Q R forms as the diameter of the circle.
Then the smallest circle will be formed by taking Q as center which should be passing through \[{\rm{P}}\left( {{\rm{a}},{\rm{ b}}} \right)\] and the largest circle will be formed by taking R as center which should be passing through P.
So the distance between their radii will be the difference between \[{\rm{PR}}-{\rm{PQ}}\]=$\text{QR}$ or QR means the diameter of the circle. As the radius of the circle is 3cm then its diameter will be \[{\rm{2}} \times {\rm{3cm}}\] or 6cm.
So the correct option is ‘B’.

Note: If two points are considered on the circumference of a circle then the max distance between them will be obtained when they are at the extremes of the diameter.