Question

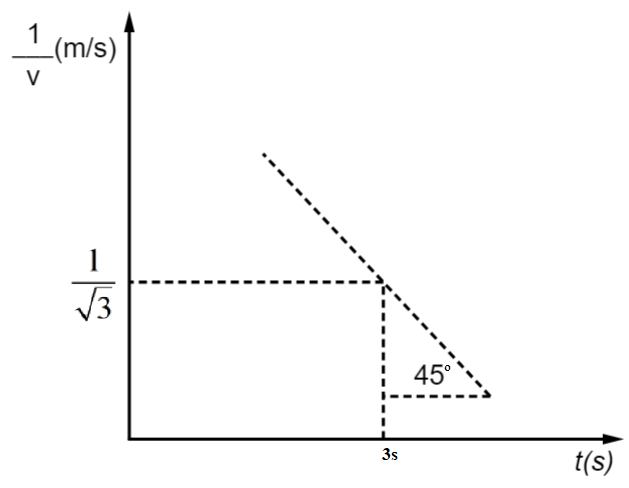
The diagram shows the variation of $\dfrac{1}{v}$ (where $v$ is the velocity of the particle) with respect to time. At time $t=3\ \text{s}$ using the details given in the graph, the instantaneous acceleration will be equal to

Answer 1

Hint: The instantaneous acceleration of a body at any instant is defined as the time derivative of the velocity of the particle at that instant. This can be mathematically written as $a=\dfrac{\text{d}v}{\text{d}t}$
Also, the slope of a curve is given as,
$m=\dfrac{\text{d}y}{\text{d}x}=\tan \theta $

Formula used:
$a=\dfrac{\text{d}v}{\text{d}t}$

Complete step by step answer:
Consider the velocity of a particle is defined as a function of time. This can be denoted as $v\left( t \right)$. The velocity function can be used to determine the velocity of the particle at any instant.
Now, instantaneous acceleration is defined as the rate of change of velocity with respect to time at any instant. This can be mathematically written as,
$a=\dfrac{\text{d}v}{\text{d}t}$
Now, the graph shows the variation of $\dfrac{1}{v}$ with respect to time. The slope of the graph can be calculated as,
$\begin{align}
  & m=\dfrac{\text{d}\left( \dfrac{1}{v} \right)}{\text{dt}} \\
 & =-\left( \dfrac{1}{{{v}^{2}}} \right)\dfrac{\text{d}v}{\text{d}t}
\end{align}$
Now, the slope is also given as the tangent of the angle made by the curve at any instant. The angle is measured between tangent to the curve and positive x-axis.
Thus,

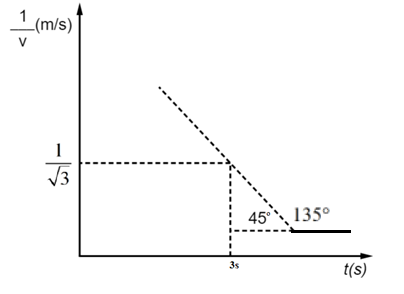
$\begin{align}
  & m=\tan \theta \\
 & =\tan \left( 180{}^\circ -45{}^\circ \right) \\
 & =\tan \left( 135{}^\circ \right) \\
 & =-1
\end{align}$
From, the two obtained equations,
$\begin{align}
  & \tan \theta =-\left( \dfrac{1}{{{v}^{2}}} \right)\dfrac{\text{d}v}{\text{d}t} \\
 & -1=-\left( \dfrac{1}{{{v}^{2}}} \right)\dfrac{\text{d}v}{\text{d}t}
\end{align}$
The aim is to find the instantaneous acceleration at $t=3\ \text{s}$. Therefore, determine the value of $\dfrac{1}{v}$ at $t=3\ \text{s}$. The graphs show ${{\left( \dfrac{1}{v} \right)}_{t=3}}=\dfrac{1}{\sqrt{3}}$. Use this value in the above obtained expression. The instantaneous acceleration is calculated as,
$\begin{align}
  & -1=-\left( \dfrac{1}{{{v}^{2}}} \right)\dfrac{\text{d}v}{\text{d}t} \\
 & -1=-{{\left( \dfrac{1}{\sqrt{3}} \right)}^{2}}\dfrac{\text{d}v}{\text{d}t} \\
 & \dfrac{\text{d}v}{\text{d}t}={{\left( \sqrt{3} \right)}^{2}} \\
 & =3\ \text{m}\cdot {{\text{s}}^{-2}}
\end{align}$
Thus, the value of instantaneous acceleration at $t=3\ \text{s}$ is $3\ \text{m}\cdot {{\text{s}}^{-2}}$.

Note: Use the rules of differentiation carefully while calculating the instantaneous acceleration. Determine the value of $\dfrac{1}{v}$ at the instant when the instantaneous acceleration is to be determined. The angle to be used to calculate the slope must be the angle between tangent and positive x-axis.