Question

The diagram shows a U-tube manometer containing three liquids: mercury, liquid X and liquid Y. Neither liquid X nor liquid Y mixes with mercury. Which row compared the pressure exerted by liquid X and by liquid Y on the mercury, and the density of liquid X and the density of liquid Y?

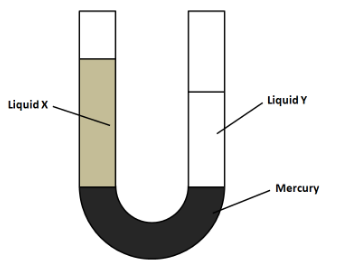
(A) Pressure exerted by X and by Y on the mercury – pressure of X is greater than Y. Densities of X and Y – density of X is greater than Y.
(B) Pressure exerted by X and by Y on the mercury – pressure of X is greater than Y. Densities of X and Y – density of Y is greater than X.
(C) Pressure exerted by X and by Y on the mercury – pressure of X and Y is the same. Densities of X and Y – density of X is greater than Y.
(D) Pressure exerted by X and by Y on the mercury – pressure of X and Y is the same. Densities of X and Y – density of Y is greater than X.

Answer 1

Hint : To solve this question, we have to use Pascal's law for the pressure inside a fluid contained in a vessel. Using this we can find out the required relations between the pressures exerted on the mercury and the densities of the two liquids.

Formula Used: The formula which is used in solving this question is given by
 $\Rightarrow P = {P_o} + \rho gh $ , here $ P $ is the pressure of a fluid column of density $ \rho $ at a point which is situated at a depth of $ h $ , and $ {P_0} $ is the atmospheric pressure.

Complete step by step answer
Let $ {h_X} $ and $ {h_Y} $ be the heights of the liquids columns X and Y respectively. Also, let $ {\rho _X} $ and $ {\rho _Y} $ be the respective densities. For the pressure exerted on the mercury, we consider the two points A and B as shown in the figure below.

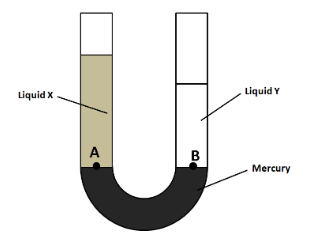
We know from Pascal's law that the pressures of a fluid at the points which are located at the same level are equal. So we have
 $\Rightarrow {P_A} = {P_B} $
Therefore, the pressure exerted by the liquids X and Y on the mercury is the same. Now, we know that the pressure of a fluid column can be written as
 $\Rightarrow P = {P_o} + \rho gh $
So from
 $ \Rightarrow {P_o} + {\rho _Y}g{h_Y} = {P_o} + {\rho _X}g{h_X} $
Subtracting $ {P_0} $ from both the sides, we get
 $\Rightarrow {\rho _Y}g{h_Y} = {\rho _X}g{h_X} $
Dividing by $ g $ both sides
 $\Rightarrow {\rho _Y}{h_Y} = {\rho _X}{h_X} $
Dividing by $ {\rho _X}{h_Y} $ both sides, we have
 $\Rightarrow \dfrac{{{\rho _Y}}}{{{\rho _X}}} = \dfrac{{{h_X}}}{{{h_Y}}} $ ……………………….(i)
From the figure in the above figure, we can clearly see that $ {h_X} > {h_Y} $ . So we have
 $\Rightarrow \dfrac{{{h_X}}}{{{h_Y}}} > 1 $
From (i) we get
 $\Rightarrow \dfrac{{{\rho _Y}}}{{{\rho _X}}} > 1 $
Or
 $\Rightarrow {\rho _Y} > {\rho _X} $
So the density of the liquid Y is greater than that of the liquid X.
Hence, the correct answer is option D.

Note
We should not try to compare the densities using the contrast of the colors in the diagram given in the question. The diagram may be represented anyway, but the final comparison will only be based on the analytical calculations only.