Question

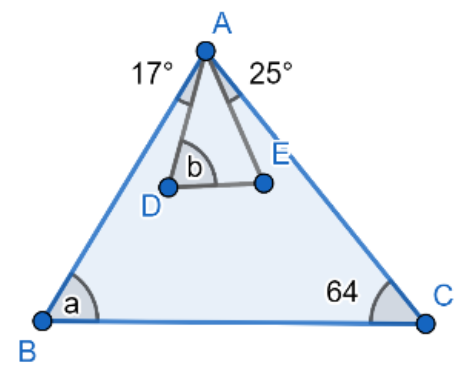
The diagram shows 2 isosceles triangles. AC = BC and AD = AE. Find the sum of a and b.

1. \[79^\circ \]
2. $58^\circ $
3. $137^\circ $
4. $140^\circ $

Answer 1

Hint: Triangle ADE and triangle ABC both are isosceles triangles. Sides AC is equal to BC and AD is equal to AE. And angle ABC will be equal to angle CAB and angle ADE will be equal to angle AED. So, using the properties of isosceles triangle and angle sum property of triangles we will find the value of a and b.

Complete step-by-step solution:
Given: AC = BC
AD = AE
$\angle ABC = \angle CAB$
$\angle ADE = \angle AED$
In triangle ABC,
By using the angle sum property of the triangle we will find the value of a.
$\angle ABC + \angle BCA + \angle CAB = 180^\circ $
Substituting the values in the above equation. Angle ABC and angle CAB are equal so, we will write both of them as a.
$a + 64^\circ + a = 180^\circ $
$\Rightarrow 2a + 64^\circ = 180^\circ $
$\Rightarrow 2a = 180^\circ - 64^\circ $
$\Rightarrow 2a = 116^\circ $
$\Rightarrow a = 58^\circ $
So, the value of a is $58^\circ $.
In triangle ADE,
$\angle DAE = \angle CAB - \angle CAE - \angle DAB$
Substituting the values in the above equation.
$\angle DAE = 58^\circ - 25^\circ - 17^\circ $
$\angle DAE = 16^\circ $
Now, by using angle sum property we will find the value of b. angle ADE and angle AED are equal. So, we can write both of them as b.
$\angle ADE + \angle DEA + \angle EAD = 180^\circ $
$\Rightarrow b + b + 16^\circ = 180^\circ $
$\Rightarrow 2b + 16^\circ = 180^\circ $
$\Rightarrow 2b = 180^\circ - 16^\circ $
$\Rightarrow 2b = 164^\circ $
$\Rightarrow b = 82^\circ $
So, the value of b is $82^\circ $.
Now, finding the sum of a and b.
$a + b = 58^\circ + 82^\circ $
$\Rightarrow a + b = 140^\circ $
The sum of a and b is $140^\circ $.
So, option (4) is the correct answer.

Note: Isosceles triangle is the triangle whose 2 sides are equal to each other and angles on the third side are equal to each other.
In this case properties of isosceles triangle and angle sum property of triangle are used to solve the problem. Students are advised to do the calculations accurately and do not miss any positive or negative sign while solving the equations.