Question

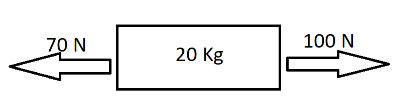
The diagram below shows the horizontal forces on a $20.0\,kg$ mass. The forces are constant in time. If the mass starts from rest, how far has it traveled in the horizontal direction after $3.00\,s$ ?

A. 4.5 m
B. 9 m
C. 6.75 m
D. 22.5 m

Answer 1

Hint: The use of force. A push or pull on an item can be characterised as a force. They can be caused by gravity, magnetism, or any other phenomenon that causes a mass to accelerate. As a result, we solve the issue using the second equation of motion.

Formula used:
\[s = ut + \dfrac{1}{2}a{t^2}\]
Here $S$ = displacement, $U$ = initial velocity, $T$ = time and $A$ = acceleration.


Complete step by step answer:
Equations of motion are physics equations that describe a physical system's behaviour in terms of its motion as a function of time. The equations of motion, more particularly, explain the behaviour of a physical system as a collection of mathematical functions expressed in terms of dynamic variables.

In physics, equations of motion are equations that describe a physical system's behaviour in terms of its motion as a function of time. Components such as displacement(s), velocity (initial and final), time(t), and acceleration may be calculated using three equations of motion (a).
\[s = ut + \dfrac{1}{2}a{t^2}\] is the second equation of motion
Hence given in the question
${F_{net}} = 100 - 70\,N$
$\Rightarrow {F_{net}} = 30\,N$
We know that $F = ma$
Here $m = 20\,kg$
Hence
$a = \dfrac{F}{m}$
$\Rightarrow a = \dfrac{{30}}{{20}}$
$\Rightarrow a = 1.5\,m{s^{ - 2}}$
Substituting them in equations of motion we get
\[s = ut + \dfrac{1}{2}a{t^2}\]
Initial velocity becomes zero.
Hence, \[s = \dfrac{1}{2}a{t^2}\]
$s = \dfrac{1}{2} \times 1.5 \times {3^2}$
\[ \therefore {\text{s }} = {\text{ }}6.75{\text{ }}m\]

Hence option C is correct.

Note:The horizontal pressures are equivalent in magnitude and direction, but they oppose each other. The horizontal resultant force is 0 since they are balanced. This means there is no horizontal acceleration and only a steady horizontal speed. The vertical pressures are equivalent in magnitude and direction, but they oppose each other.