Question

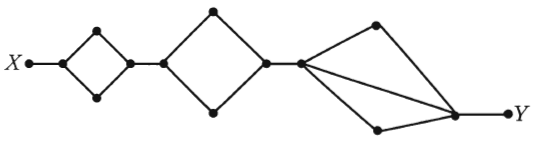
The diagram above shows the various paths along which a mouse can travel from point X, where it is released to point Y, where it is rewarded with a food pellet. How many different paths from X to Y can the mouse take if it goes directly from X to Y without retracing any point along a path?

Answer 1

Hint: Here the given question need to find the many possible path available for the mouse in order to complete its path from X to Y, here we need to solve it by seeing the different variation that can be obtained in order to reach the last point Y from the first point X.
Formulae Used: \[^n{C_m} = \dfrac{{n!}}{{m!(n - m)!}}\] here (!) represents factorial.

Complete step by step solution:
Here the possibilities for the mouse can be calculated using the combination formula, counting each path would be a long process so here we will use the combination formulae to get all the possibilities, on solving we get:
Here we have three junctions where the path for the mouse is varying, hence for every junction we need to find the maximum possible path.
 \[
   \Rightarrow Junction\,name = A,B,C \\
   \Rightarrow possibilities: \\
   \Rightarrow A = 2 \\
   \Rightarrow B = 2 \\
   \Rightarrow C = 3 \\
   \Rightarrow total\,combination{ = ^2}{C_1}{ . ^2}{C_1}{ . ^3}{C_1} = 2 \times 2 \times 3 = 12 path \;
 \]
 \[{ \Rightarrow ^2}{C_1} = \] 2, because the maximum possible path for junction “A” is two, 1 because we have to give one path to the mouse.
 \[{ \Rightarrow ^2}{C_1} = \] 2, because the maximum possible path for junction “B” is two, 1 because we have to give one path to the mouse.
 \[{ \Rightarrow ^3}{C_1} = \] 3, because the maximum possible path for junction “C” is three, 1 because we have to give one path to the mouse.
Here we know that using combination property we have to see the two parameter one is the required selection, here for this question is “one” because we need to choose one path only, and the second one is the total possibility we can have for the selection, for this question we have two for “A and B” junction, and three for the “C” junction.
Hence total 12 paths are possible for a mouse.
So, the correct answer is “12 paths”.

Note: Here we have used a combination rule to solve for the maximum possible path, but we can also solve it by counting each possible path, by numbering all the paths and then by writing each possible path we can reach to the maximum possible path.