Question

The diagonals of a rhombus are 12cm and 7.5cm. Find its area.

Answer 1

Hint: Use the fact that the diagonals of a rhombus bisect each other at right angles. Using the property that the area of a triangle with base b and height h is given by $\dfrac{1}{2}bh$. Hence find the area of each of the triangles in which the rhombus is divided by the diagonals. Hence find the area of the rhombus. Alternatively, use the fact that the area of the rhombus with diagonals ${{d}_{1}}$ and ${{d}_{2}}$ is given by $\dfrac{1}{2}{{d}_{1}}{{d}_{2}}$. Hence determine the area of the rhombus.

Complete step-by-step answer:

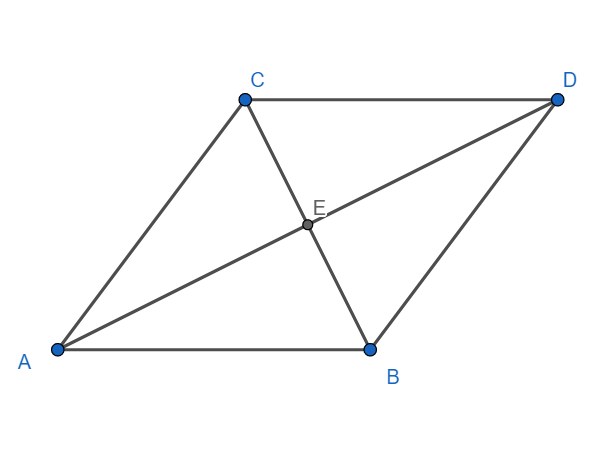
Consider the rhombus ABCD, with AD = 12cm and BC = 7.5cm.
Since the diagonals of a rhombus bisect each other, we have
$CE=\dfrac{7.5}{2}=3.75=BE$ and $AE=\dfrac{12}{2}=6=DE$.
Now, we have
In the triangle DEC $DE\bot CE$(diagonals of a rhombus are perpendicular to each other).
Hence, we have
$ar\left( \Delta DEC \right)=\dfrac{1}{2}\times DE\times CE=\dfrac{1}{2}\times 6\times 3.75=11.25$
Similarly, we have
$ar\left( \Delta BEC \right)=ar\left( \Delta AEB \right)=ar\left( \Delta AEC \right)=11.25$
The area of the rhombus ABCD is the sum of the area of the triangle AEB, AEC, DEC and DEB
Hence, we have
$ar\left( ABCD \right)=11.25+11.25+11.25+11.25=4\times 11.25=45$
Hence the area of the rhombus ABCD = 45 square centimetres.

Note: Alternatively, we know that the area of a rhombus with diagonals ${{d}_{1}}$ and ${{d}_{2}}$ is given by $\dfrac{1}{2}{{d}_{1}}{{d}_{2}}$
Here, we have
${{d}_{1}}=12cm$ and ${{d}_{2}}=7.5cm$
Hence, the area of rhombus
$=\dfrac{1}{2}\left( 12 \right)\times \left( 7.5 \right)=45$ square centimetres, which is the same as obtained above.