Question

The diagonal of a square is 12 cm long, find the value of its area

Answer 1

Hint: Area is the quantity that expresses the extent of a two-dimensional figure or shape or planar lamina, in the plane. In mathematics, the unit square is defined to have area one, and the area of any other shape or surface is a dimensionless real number. Some examples of square units in metric units are square meters, square centimetres, and in customary units are square inches, square feet. Square Units are often confused with Unit Squares. A unit square is a square with sides measuring 1 unit, while square units is a unit of measurement.

Complete step-by-step answer:
In geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, or 100 -gradian angles or right angles). It can also be defined as a rectangle in which two adjacent sides have equal length.
To find the area of a rectangle, multiply its height by its width. For a square we only need to find the length of one of the sides (as each side is the same length) and then multiply this by itself to find the area.
Let the side of the square = a cm

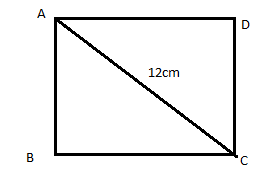
The diagonal of a square divides it into two equal right-angled triangles.
Hence, diagonal forms the hypotenuse of a right-angled triangle with the other
two sides being the sides of the square. Hence, diagonal $=\sqrt{\mathrm{a}^{2}+\mathrm{a}^{2}}=12
\mathrm{~cm}
=>2 \mathrm{a}^{2}=144
=>\mathrm{a}^{2}=72
=>\mathrm{a}=6 \sqrt{2}$
Area of the square $=\mathrm{a}^{2}
=(6 \sqrt{2})^{2}
=72 \mathrm{sq} \mathrm{cm}$.

Note: The line stretching from one corner of the square or rectangle to the opposite corner through the centre of the figure is known as the diagonal. Any square that has two diagonals are equal in length to each other. To find the length of the diagonal of a square, multiply the length of one side by the square root of 2: If the length of one side is x. The diagonals of a square intersect (cross) in a 90-degree angle. This means that the diagonals of a square are perpendicular.
A square has two diagonals, which are line segments linking opposite vertices (corners) of the square. Each one is a line segment drawn between the opposite vertices (corners) of the square. The diagonals have the following properties: The two diagonals are congruent (same length).