Question

The curved surface area of a hemisphere of diameter $ 2r $ is \[\]
A. $ 2\pi {{r}^{2}} $ \[\]
B. $ 3\pi {{r}^{2}} $ \[\]
C. $ 4\pi {{r}^{2}} $ \[\]
D. $ 8\pi {{r}^{2}} $ \[\]

Answer 1

Hint: We recall the shape of a sphere and a hemisphere. We recall that the hemisphere is obtained when a plane cuts through the diameter of a sphere into two equal halves. So we take half of the curved surface area of a sphere to get the curved surface area of a hemisphere. \[\]

Complete step by step answer:
We know that sphere is a locus of points in space that are equal distance from a fixed point. The fixed point is called center. The line segment that passes through the centre of the sphere is called the diameter of the sphere and the line segment joining the centre of the sphere to a point of the sphere is called the radius, commonly denoted as $ r $ . \[\]

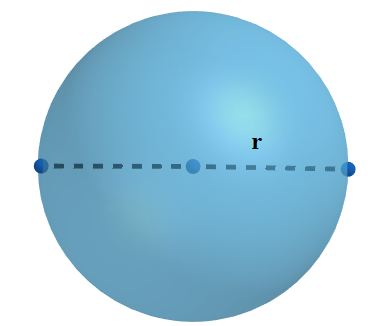
The amount of region covered by the outer surface of the sphere is called the curved surface area of the sphere and the curved surface area (CSA) of the sphere is given by
\[\text{CSA}=4\pi {{r}^{2}}\]
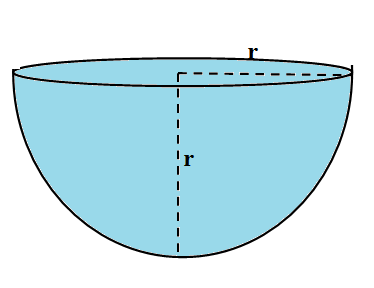
We know that a hemisphere is obtained when we cut a sphere into two equal halves with a plane containing the center of the sphere. So the surface of the sphere will be cut into two equal halves. So the curved surface area of the hemisphere will be half of the surface area of the sphere that means with radius $ r $ as;
\[\text{CSA}=\dfrac{1}{2}\left( 4\pi {{r}^{2}} \right)=2\pi {{r}^{2}}\]
We are asked in the question to find the curved surface area of a hemisphere with diameter $ 2r $ We know the radius is always half of the diameter. So the radius of the given hemisphere is $ \dfrac{2r}{r}=r $ . We find the curved surface area of the given hemisphere with radius $ r $ as;
 \[\text{CSA}=2\pi {{\left( r \right)}^{2}}=2\pi {{r}^{2}}\]
 So the correct option is A.\[\]

Note:
We note that a hemisphere has both curbed and plane surface area. We have only calculated here curved surface area. The plane surface area of the hemisphere is a circular surface with radius $ r $ which is given by $ \pi {{r}^{2}} $ and the total surface area is the areas of curved and plane surface that is $ 2\pi {{r}^{2}}+\pi {{r}^{2}}=3\pi {{r}^{2}} $ .